Chapter 4: The Integral
Section 4.3: Antiderivatives of Formulas
Learning Objectives
By the end of this section, the student should be able to:
- Use antiderivative rules to find indefinite integrals.
- Evaluate definite integrals using the fundamental theorem of calculus.
- Use definite integrals to solve real-life problems.
Building Blocks
Antidifferentiation is going backward through the derivative process. So the easiest antiderivative rules are simply backwards versions of the easiest derivative rules.
Recall from Chapter 2:
Key Takeaways
Derivative Rules: Building Blocks
In what follows, [latex]f[/latex] and [latex]g[/latex] are differentiable functions of [latex]x[/latex].
Constant Multiple Rule
[latex]\frac{d}{dx}\left( kf\right)=kf’[/latex]
Sum and Difference Rule
[latex]\frac{d}{dx}\left(f\pm g\right)=f' \pm g'[/latex]
Power Rule
[latex]\frac{d}{dx}\left(x^n\right)=nx^{n-1}[/latex]
Special Cases
[latex]\frac{d}{dx}\left(k\right)=0 \quad \text{(Because \( k=kx^0 \).)}[/latex]
[latex]\frac{d}{dx}\left(x\right)=1 \quad \text{(Because \( x=x^1 \).)}[/latex]
Exponential Functions
[latex]\frac{d}{dx}\left(e^x\right)=e^x[/latex] [latex]\frac{d}{dx}\left(a^x\right)=\ln(a)\,a^x[/latex]
Natural Logarithm
[latex]\frac{d}{dx}\left(\ln(x)\right)=\frac{1}{x}[/latex]
Thinking about these basic rules was how we came up with the antiderivatives of [latex]2x[/latex] and [latex]e^x[/latex] before.
The corresponding rules for antiderivatives are next – each of the antiderivative rules is simply rewriting the derivative rule. All of these antiderivatives can be verified by differentiating.
There is one surprise: the antiderivative of [latex]\frac{1}{x}[/latex] is actually not simply [latex]\ln(x)[/latex]; it’s [latex]\ln|x|[/latex]. This is a good thing – the antiderivative has a domain that matches the domain of [latex]\frac{1}{x}[/latex], which is bigger than the domain of [latex]\ln(x)[/latex], so we don’t have to worry about whether our [latex]x[/latex]‘s are positive or negative. But we must be careful to include those absolute values – otherwise, we could end up with domain problems.
Video
Key Takeaways
Antiderivative Rules: Building Blocks
In what follows, [latex]f[/latex] and [latex]g[/latex] are differentiable functions of [latex]x[/latex], and [latex]k[/latex], [latex]n[/latex], and [latex]C [/latex] are constants.
Constant Multiple Rule
[latex]\int k\cdot f(x)\, dx=k\cdot\int f(x)\, dx[/latex]
Sum and Difference Rule
[latex]\int \left(f(x)\pm g(x)\right)\, dx=\int f(x)\, dx \pm \int g(x)\, dx[/latex]
Power Rule
[latex]\int x^n \, dx = \frac{x^{n+1}}{n+1}, \text{ provided that } n\neq -1[/latex]
Special case: [latex]\int k\, dx =kx+C \quad \text{(Because \( k=kx^0 \).)}[/latex] (The other special case, [latex]( n=-1 )[/latex], is covered next.)
Natural Logarithm
[latex]\int x^{-1}\, dx =\int\frac{1}{x}\, dx = \ln|x|+C[/latex]
Exponential Functions
[latex]\int e^x\, dx=e^x +C[/latex] [latex]\int a^x\, dx = \frac{a^x}{\ln(a)}+C[/latex]
Example 1
Find the antiderivative of [latex]y=3x^7-15\sqrt{x}+\frac{14}{x^2}[/latex].
[latex]\begin{align*} \int\left( 3x^7-15\sqrt{x}+\frac{14}{x^2} \right)\, dx=& \int\left( 3x^7-15x^{1/2}+14x^{-2} \right)\, dx \\ =& 3\frac{x^8}{8}-15\frac{x^{3/2}}{3/2}+14\frac{x^{-1}}{-1}+C \\ =& \frac{3}{8}x^8-10x^{3/2}-14x^{-1}+C \end{align*}[/latex]
Example 2
Find [latex]\int\left(e^x+12-\frac{16}{x}\right)\, dx[/latex].
[latex]\int\left(e^x+12-\frac{16}{x}\right)\, dx =e^x+12x-16\ln|x|+C[/latex]
Example 3
Find [latex]F(x)[/latex] so that [latex]F'(x)=e^x[/latex] and [latex]F(0)=10[/latex].
This time we are looking for a particular antiderivative; we need to find exactly the right constant. Let’s start by finding the antiderivative: [latex]\int e^x\, dx=e^x+C[/latex]
So we know that [latex]F(x)=e^x+\text{(some constant)}[/latex]; now we just need to find which one. To do that, we’ll use the other piece of information (the initial condition):
[latex]\begin{align*} F(x)=& e^x+C \\ F(0)=& e^0+C=1+C=10 \\ C=& 9 \end{align*}[/latex]
The particular constant we need is 9; thus, [latex]F(x)=e^x+9[/latex].
Video
The reason we are looking at antiderivatives right now is so we can evaluate definite integrals exactly. Recall the fundamental theorem of calculus:
[latex]\int\limits_a^b F'(x)\, dx = F(b)-F(a)[/latex]
If we can find an antiderivative for the integrand, we can use that to evaluate the definite integral. The evaluation [latex]F(b) - F(a)[/latex] is represented as [latex]\left.F(x)\right]_a^b[/latex] or [latex]\left.F(x)\right|_a^b[/latex].
Example 4
Evaluate [latex]\int\limits_1^3 x[/latex], dx in two ways:
- By sketching the graph of [latex]y = x[/latex] and geometrically finding the area.
- By finding an antiderivative of [latex]F(x)[/latex] of the integrand and evaluating [latex]F(3)-F(1)[/latex].
- The graph of [latex]y = x[/latex] is shown below, and the shaded region corresponding to the integral has area 4.
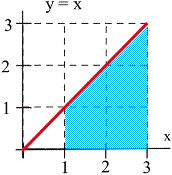
- One antiderivative of [latex]x[/latex] is [latex]F(x)=\frac{1}{2}x^2[/latex], and
[latex]\begin{align*} \int\limits_1^3 x\, dx =& \left[\frac{1}{2}x^2\right]_1^3 \\ =& \left(\frac{1}{2}(3)^2\right) - \left(\frac{1}{2}(1)^2\right) \\ =& \frac{9}{2}-\frac{1}{2} \\ =& 4. \end{align*}[/latex]
Note that this answer agrees with the answer we got geometrically. If we had used another antiderivative of x, say [latex]F(x)=\frac{1}{2}x^2+7[/latex], then
[latex]\begin{align*} \int\limits_1^3 x\, dx =& \left[\frac{1}{2}x^2+7\right]_1^3 \\ =& \left(\frac{1}{2}(3)^2+7\right) - \left(\frac{1}{2}(1)^2+7\right) \\ =& \frac{9}{2}+7-\frac{1}{2}-7 \\ =& 4. \end{align*}[/latex]
In general, whatever constant we choose gets subtracted away during the evaluation, so we might as well always choose the easiest one, where the constant is 0.
Example 5
Find the area between the graph of [latex]y = 3x^2[/latex] and the horizontal axis for [latex]x[/latex] between 1 and 2.
This is [latex]\int\limits_1^2 3x^2\, dx = \left.x^3\right|_1^2 = 2^3-1^3 = 7.[/latex]
Video
Example 6
A robot has been programmed so that when it starts to move, its velocity after [latex]t[/latex] seconds will be [latex]3t^2[/latex] feet/second.
- How far will the robot travel during its first 4 seconds of movement?
- How far will the robot travel during its next 4 seconds of movement?
- The distance during the first 4 seconds will be the area under the graph of velocity, from [latex]t = 0[/latex] to [latex]t = 4[/latex].
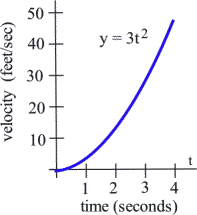
That area is the definite integral [latex]\int\limits_0^4 3t^2\, dt[/latex]. An antiderivative of [latex]3t^2[/latex] is [latex]t^3[/latex], so [latex]\int\limits_0^4 3t^2\, dt =\left. t^3 \right]_0^4 =4^3-0^3 =[/latex] 64 feet.
- [latex]\int\limits_4^8 3t^2\, dt =\left. t^3 \right]_4^8=8^3-4^3 =512 - 64 =[/latex] 448 feet.
Example 7
Suppose that [latex]t[/latex] minutes after putting 1000 bacteria on a Petri plate, the rate of growth of the population is [latex]6t[/latex] bacteria per minute.
- How many new bacteria are added to the population during the first 7 minutes?
- What is the total population after 7 minutes?
- The number of new bacteria is the area under the rate of growth graph, and one antiderivative of [latex]6t[/latex] is [latex]3t^2[/latex].
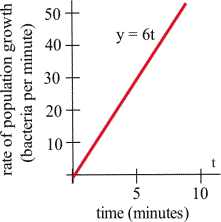
So [latex]\text{new bacteria}=\int\limits_0^7 6t\, dt= \left. 3t^2\right|_0^7=3(7)^2-3(0)^2=147[/latex]
- The new population = (old population) + (new bacteria) = 1000 + 147 = 1147 bacteria.
Video
Example 8
A company determines their marginal cost for production, in dollars per item, is [latex]MC(x)=\frac{4}{\sqrt{x}}+2[/latex] when producing [latex]x[/latex] thousand items. Find the cost of increasing production from 4 thousand items to 5 thousand items.
Remember that marginal cost is the rate of change of cost, and so the fundamental theorem tells us that [latex]\int\limits_a^b MC(x)\, dx = \int\limits_a^b C'(x)\, dx = C(b)-C(a)[/latex]. In other words, the integral of marginal cost will give us a net change in cost. To find the cost of increasing production from 4 thousand items to 5 thousand items, we need to integrate [latex]\int\limits_4^5 MC(x)\, dx[/latex].
We can write the marginal cost as [latex]MC(x)=4x^{-1/2}+2[/latex]. We can then use the basic rules to find an antiderivative: [latex]C(x)=4\frac{x^{1/2}}{1/2}+2x=8\sqrt{x}+2x.[/latex]
Using this,
[latex]\begin{align*} \text{Net change in cost }=& \int\limits_4^5 \left(4x^{-1/2}+2\right)\, dx \\ =& \left[ 8\sqrt{x}+2x \right]_4^5 \\ =& \left( 8\sqrt{5}+2(5) \right)-\left( 8\sqrt{4}+2(4) \right) \\ \approx& 3.889 \end{align*}[/latex]
It will cost 3.889 thousand dollars to increase production from 4 thousand items to 5 thousand items. (The final answer would be better written as $3889.)

