Chapter 3: Applications of the Derivative
Chapter 3 Solutions to Review Problems
Chapter 3 Solutions to Review Problems
1.
[latex]f(x) = x^2-10x+3[/latex], so [latex]f'(x) = 2x-10[/latex]. [latex]f[/latex] has horizontal tangents where [latex]f'(x)=0[/latex], so [latex]f[/latex] has a horizontal tangent at [latex]x = 5[/latex]. [latex]g(x) = x^3-12x[/latex], so, [latex]g'(x) = 3x^2-12[/latex]. [latex]g[/latex] has horizontal tangents at [latex]x =-2[/latex] and at [latex]x =2[/latex].
3.
a. [latex]h'(x) = -32x+128[/latex]. When [latex]x=0[/latex], the velocity is [latex]128[/latex] ft/sec (of course), when [latex]x = 1[/latex], the velocity is [latex]96[/latex] ft/sec, and when [latex]x = 2[/latex], the velocity is [latex]64[/latex] ft/sec.
b. [latex]v(x) = h'(x) = -32x+ 128[/latex].
c. The velocity is zero when [latex]x = 4[/latex]; the velocity is zero [latex]4[/latex] seconds after the arrow is shot.
d. The greatest height is the vertex of the parabola (also where velocity [latex]= 0[/latex]), when [latex]x = 4[/latex] seconds. After [latex]4[/latex] seconds, the arrow is [latex]256[/latex] feet high.
e. The arrow will be aloft until it hits the ground until its height is zero. Solving [latex]h(x) = 0[/latex] gives [latex]x = 0[/latex] (when the arrow is shot) and [latex]x = 8[/latex] (when the arrow comes back to the ground). The arrow is aloft for [latex]8[/latex] seconds.
f. [latex]a(x) = v’(x) = h' ' (x) = -32.[/latex] The acceleration is a constant [latex]32[/latex] ft/sec2, the acceleration due to gravity.
5.
[latex]\frac{d}{dx} \bigg( (x^2+2x+2)^{12} \bigg) = 12(x^2+2x+2)^{11}(2x+2)[/latex]; at [latex]a= 0, y= 2^{12} = 4096[/latex] and [latex]y' = 12(2^{11})(2)= 49512[/latex]. The equation of the tangent line is [latex]y-4096= 49512(x-0)[/latex], or [latex]y=49512x+4096[/latex].
7.
[latex]\frac{d}{dx}\bigg(x+\frac{1}{x}\bigg)^2=2\bigg(x+\frac{1}{x}\bigg)\bigg(x-\frac{1}{x^2}\bigg); a=0.5, y=6.25[/latex] and [latex]y'=-15[/latex]. The equation of the tangent line is [latex]y-6.25 = -15(x-0.5).[/latex]
9.
[latex]\frac{d}{dx}(e^x+e^{-x}) = e^x - e^{-x} ; at a=0, y= 2[/latex] and [latex]y'=0[/latex]. The equation of the tangent line is [latex]y=2[/latex].
10.
a. A beginning employee has [latex]d = 0[/latex] days of production experience, so his production will be about [latex]P(0) = 3 +15 (1-e^{-0.2d}) = 3[/latex] items per day.
b. As [latex]d \rightarrow \infty[/latex], the exponential part of this function will [latex]\rightarrow 0[/latex]; an experienced employee will be approaching [latex]18[/latex] items per day.
c. Marginal production is the derivative, [latex]P'(d) = 15(0.2e^{-0.2d})[/latex]. When [latex]d = 5, P(5)[/latex]= about [latex]1.1[/latex] items per day per day. That is, when the employee has [latex]5[/latex] days of experience, her production is increasing by a little more than one item per day each day.
12.
[latex]y' = 3Ax^2[/latex]
14.
[latex]y= \sqrt{A+Bx^2} = (A+Bx^2)^{\frac{1}{2}} , so \frac{dy}{dx} = \frac{1}{2} \bigg(( A+Bx^2)^{-\frac{1}{2}} \bigg) (2Bx) = \frac{Bx}{\sqrt{A+Bx^2}}[/latex]
16.
[latex]y'= ABe^{Bx}[/latex]
49.
[latex]\frac{dy}{dx} = \frac{(A)(Cx+D)-(C)(Ax+B)}{(Cx+D)^2} = \frac{AD-CB}{(Cx+D)^2}[/latex]
22.
[latex]y = \frac{1}{\ln(Ax+B)} =(\ln(Ax+B))^{-1}[/latex], so
[latex]y'= - (\ln(Ax+B))^{-2}( \frac{1}{Ax+B} )(A) = \frac{-A}{(Ax+B)(\ln(Ax+B))^2}[/latex]
24.
[latex]y=\frac{1}{\frac{1}{\ln(Ax+B)}}*\frac{-1}{(Ax+B)^2}*1=\frac{-A}{Ax+B}[/latex]. Alternatively, you can write
[latex]\ln \bigg(\frac{1}{Ax=B}\bigg)=\ln(Ax+B)^{-1}=-\ln(Ax+B)[/latex]; then[latex]\frac{dy}{dx}=\frac{-1}{Ax+B}*A=\frac{-A}{Ax+B}.[/latex]
26.
a. [latex]y' = AB - 2Ax[/latex]
b. [latex]y'=0[/latex] when [latex]x = \frac{B}{2}[/latex] ( provided [latex]A \neq 0 )[/latex].
c. [latex]y' ' = -2A.[/latex]
28.
a. The quantity that is changing is “unemployment.” The units of unemployment are not stated. Let [latex]f(t)[/latex] be the unemployment after t months. The statement says that [latex]f'[/latex] is positive, but [latex]f' '[/latex] is negative.
b. The quantity is profits. Let [latex]f(t)[/latex] be profit in dollars after [latex]t[/latex] months. The statement says [latex]f’[/latex] is negative, but [latex]f’’[/latex] is positive ([latex]f’[/latex] is getting less negative, so [latex]f’[/latex] is increasing).
c. The quantity is population. Let [latex]f(t)[/latex] be the population in millions of people after [latex]t[/latex] years. The statement says [latex]f’[/latex] is positive, and [latex]f' '[/latex] is positive.
30.
The function is concave down on [latex](0,3)[/latex] and concave up on [latex](3,7)[/latex].
31.
Answers will vary. Here are some examples:
a.
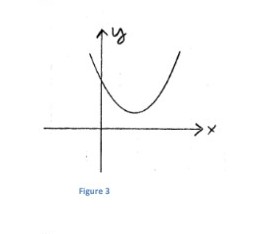
b.
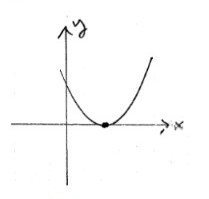
c.
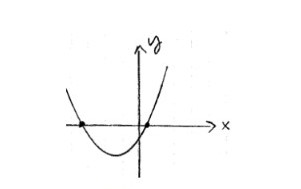
d.
This can’t be done if the function really is concave up everywhere. Here is an example where the function is concave up everywhere except one point (the cusp).
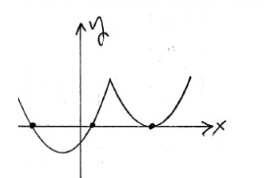
34.
[latex]g(x) = x^3-3x^2-9x+7 ; g'(x) = 3x62-6x-9; g' '(x) = 6x-6[/latex].
At [latex]x = -1; g' '(-1) = -12 < 0[/latex]; there is a local maximum at [latex](-1,12)[/latex]. At[latex]x = 3, g' '(x) = 12 > 0[/latex], there is a local minimum at [latex](3, -20)[/latex].
36.
[latex]f(x) = x \ln(x), f'(x) = \ln(x) +1; f' '(x) = \frac{1}{x}.[/latex]
[latex]f''(\frac{1}{e}) = e > 0[/latex]; so there is a local minimum at [latex](\frac{1}{e} , \frac{1}{e} )[/latex].
38.
The function seems to have points of inflection at b, d, and h. Note that the cusp [latex]f[/latex] is not an inflection point, since the function is concave up on both sides.
40.
| [latex]x[/latex] | [latex]f(x)[/latex] | [latex]f'(x)[/latex] | [latex]f' '(x)[/latex] |
|---|---|---|---|
| [latex]0[/latex] | [latex]+[/latex] | [latex]+[/latex] | [latex]-[/latex] |
| [latex]1[/latex] | [latex]+[/latex] | [latex]-[/latex] | [latex]+[/latex] |
| [latex]2[/latex] | [latex]+[/latex] | [latex]0[/latex] | [latex]+[/latex] |
| [latex]3[/latex] | [latex]+[/latex] | [latex]+[/latex] | [latex]0[/latex] |
42.
[latex]f'(x) = 14x = 5; f'(x) = 14.[/latex]
44.
[latex]f'(x) = 10 (2x^3+3)^5(6x^2);[/latex]
[latex]f' '(x) = 10( 9( 6x-x^2)^8)(6-2x) + (6x-x^2)^9(-2))[/latex]
[latex]= 20 (6x-x^2)^8(x^2-15x+27)[/latex]
(I’m simplifying so you can recognize your answer if you did this problem a different way.)
46.
[latex]f'(x) = 6 (6x-x^2)^9(6-2x);[/latex]
[latex]f' '(x) = 6( 5( 2x^3+3)^4)(6x^2) + (2x^3+3)^{5}(12x))[/latex]
[latex]= 6(2x+3)^4(24x^3+30x+36).[/latex]
48.
[latex]f'(x) = \frac{1}{x^2+4} * 2x = \frac{2x}{x^2+4}; \ f' '(x) = \frac{2(x^2+4)- 2x(2x)}{(x^2+4)^2} = \frac{8-2x^2}{x^2+4}[/latex].
50.
First, find critical points: [latex]f'(x) = 6x -12 = 0[/latex] when [latex]x = 2[/latex]; this is the only critical point. As we move from left to right near [latex]x = 2, f'[/latex] goes from negative to positive; this point is a local minimum. The function has a local minimum at the point [latex](2, −5)[/latex].
52.
[latex]f'(x) = 4x-12; f[/latex] has one critical point, where [latex]x = 3[/latex]. At [latex]x = 3, f '[/latex] changes from negative to positive, so this critical point is a local minimum. The only local extremum of [latex]f[/latex] is a local minimum at [latex](3, −11)[/latex].
54.
[latex]f'(x) = 2(x-1)(x-3) + (x-1)^2 = 3x^2-10x + 7; f'(x) =0[/latex] when [latex]x = \frac{7}{3}[/latex] or [latex]x = 1[/latex]. At [latex]x = \frac{7}{3} \ ; f' ' (x) = 4 > 0[/latex]; there is a local minimum at [latex]( \frac{7}{3} , -\frac{32}{37} )[/latex]. At [latex]x = 1, f' ' (x) = -4 < 0[/latex]; there is a local maximum at [latex](1,0)[/latex]. 56. [latex]f'(x) = 6x^2-96 = 6(x^2-16)[/latex]; there are critical points at [latex]x = 4[/latex] and [latex]x = -4. f' '(x) = 12x[/latex]. At [latex]x = 4, \ f' '(x) >0[/latex]; there is a local minimum at [latex](4,-214)[/latex].
58.
[latex]f'(x) = - 3x^2[/latex], so the only critical point is [latex](0, 2)[/latex]. The second derivative test fails here, but the first derivative test works – the first derivative is negative on both sides of the critical point, so this point is either a maximum or a minimum. This function has neither a global minimum nor a global maximum on the entire real number line.
60.
[latex]f'(x) = 1 - e^x ; \ f' '(x) = - e^x[/latex]. The only critical point is [latex](0, −1)[/latex]. The second derivative test tells us that this point is a local maximum. Since this is the only critical point, it is the global maximum and there is no global minimum on the entire real number line.
62.
The only critical point is [latex](0, 2)[/latex], which we have seen is neither a min nor a max. So turn to the endpoints: [latex]f(-2) = 10[/latex] and [latex]f(1)= 1[/latex]. On the interval [latex][ −2, 1], f [/latex] has a global max at [latex]x = −2[/latex] and a global min at [latex]x = 1[/latex].
64.
The only critical point is [latex](0, −1)[/latex], but that point does not lie in the interval [latex][1, 2][/latex]. So turn to the endpoints: [latex]f(1) = 1- e \approx -1.718[/latex] and [latex]f(2) = 2 - e^2 \approx -5.389[/latex]. On the interval [latex][1, 2], f[/latex] has a global max at [latex]x = 1[/latex] and [latex]x = 2.[/latex]
66.
The critical points are at [latex]x = 2, 3, 5, 8.2,[/latex] and [latex]11[/latex]. There is a local min at [latex]x = 2[/latex] and [latex]x = 8.2[/latex], local max at [latex]x = 5[/latex] and [latex]x = 11[/latex]; the critical point at [latex]x = 3[/latex] is neither a local max nor min. The global max occurs at [latex]x = 0[/latex] and [latex]x = 5[/latex]; the global min is at [latex]x = 8.2[/latex].
68.
The derivative of a quadratic is linear, the second derivative is constant, the third derivative (and all higher derivatives) are zero.
70. Each time you take the derivative of a polynomial, its degree decreases by one. If you take [latex]n[/latex] derivatives of a polynomial of degree [latex]n[/latex], it has degree [latex]0[/latex]; it is constant. From that point on, each further derivative will be zero.
72.
As [latex]x[/latex] increases, the area increases. So
(a) [latex]A(x)[/latex] is minimum when [latex]x = 0[/latex], and
(b) [latex]A(x)[/latex] is maximum when [latex]x = 10[/latex].
74.
a.
Let [latex]x[/latex] be the width of the garden. Then the height of the garden is [latex]\frac{1}{2}(200-2x) = 100- x[/latex]. The area of the garden is [latex]A(x) = x (100-x)[/latex]; this is what we want to maximize. Whack it with calculus: [latex]A'(x) = 100-2x = 0[/latex]; when [latex]x = 50[/latex]; [latex]A' '(x) = - 2 <0[/latex], so this is a maximum. It’s the only critical point, so it is the global maximum. The area is maximized when [latex]x = 50[/latex] feet and [latex]y = 50[/latex] feet, or when the garden is square. c. Let [latex]x[/latex] be the width of the garden. Then the height of the garden is [latex]\frac{1}{2}(P-x)[/latex]. The area of the garden is [latex]A(x) = \frac{1}{2}(Px-x^2)[/latex]. This is what we want to minimize. Whack it with calculus: [latex]A'(x) = \frac{1}{2}(P-2x)=0[/latex]; when [latex]x = \frac{P}{2}[/latex]; [latex]A' '(x) = - 1 <0[/latex], so this is a maximum. It’s the only critical point, so it is the global maximum. The area is maximized when [latex]x = \frac{P}{2}[/latex] feet * [latex]\frac{P}{4}[/latex] feet. 76. Let [latex]x[/latex] be the height of the pen. There are [latex]5[/latex] edges of length [latex]x[/latex]. The width of the pen is [latex]\frac{1}{2} ( 20-5x) = 60-2.5x[/latex]. The area of the pen, which is what we want to maximize, is [latex]A(x) = 60x -2.5x^2, A'(x) = 60-5x = 0[/latex], when [latex]x = 12. A''(x) = - 5 < 0,[/latex] so this is a local maximum. It’s the only critical point, so it is the global maximum. The area is maximized when the outside dimensions are [latex]12[/latex] feet × [latex]30[/latex] feet; the maximum area is [latex]360[/latex] square feet. 78. The box is still square-bottomed, open top, and we still assume that no material is wasted. Let [latex]x[/latex] be the length of one of the sides of the square base, and let [latex]h[/latex] be the height of the box. We know the volume is [latex]100[/latex] cubic inches, so [latex]100- x^2h[/latex] or [latex]h = \frac{100}{x^2}[/latex]. We’re trying to minimize the cost here. The cost of the bottom is [latex].05x^2[/latex] dollars, each of the [latex]4[/latex] walls costs [latex]0.3xh = 0.3x \frac{100}{x^2} = \frac{3}{x}[/latex] dollars. so the total cost of the box is [latex]C(x) = 0.5x^2 +\frac{12}{x}[/latex]; this is the function we need to minimize; this is the function we need to minimize. Whack it with calculus: [latex]C'(x) = 0.1x - \frac{12}{x^2}[/latex]. [latex]C[/latex] has critical points when [latex]x = 0[/latex] (there is no box, we can eliminate this or when [latex]x = \sqrt[3]{120} \approx 4.93. C' '(x) = 0.1 + \frac{24}{x^3} >0[/latex] for any positive [latex]x[/latex], so this critical point is a minimum. Cost is minimized when the base of the box is about [latex]4.93” × 4.93”[/latex] and the height is about [latex]4.11”[/latex].
80.
(b) Let [latex]x[/latex] be the shorter dimension of the rectangular end; then the longer dimension is [latex]2x[/latex], the girth is [latex]6x[/latex], and the length of the box is [latex]108-6x[/latex]. The volume, which is what we're trying to maximize, is [latex]V(x) = 2x^2(108-6x) = 216x^2-12x^3[/latex]. Whack it with calculus: [latex]V'(x) = 422x - 36x^2 = 0[/latex] when [latex]x = 0[/latex] (no box, we can ignore this one) and when [latex]x = 12[/latex]. [latex]V' '(x) = 432-72(12) < 0[/latex] so this is a maximum. The volume is maximized when the base is [latex]12” × 24” × 36”.[/latex] 82. Profit is revenue minus costs. Let [latex]q[/latex] be the number of passengers. Note the domain restrictions: [latex]10 \leq q \leq 20[/latex]. The total cost is [latex]C(q) = 100 +6 q[/latex] dollars The revenue is [latex]R(q) = (30-(q-10))q = 40q - q^2[/latex] dollars. So the profit is [latex]\pi (q) = -q^2+34q - 100[/latex] dollars. This is the function we want to maximize. Calculus to the rescue: [latex]\pi '(q) = -2q + 34 = 0[/latex] when [latex]q = 17[/latex]. At [latex]q = 17 \pi ' π[/latex]’ changes from positive to negative, so this is a local maximum. This is the only critical point, so this is the global maximum. Profit is maximized if we carry [latex]17[/latex] passengers. 84. First, note that if we have fewer than [latex]80[/latex] people, adding another seat will definitely increase our profit. So any maximum must occur for a larger coffee shop. If we let q be the number of seats in our coffee shop, we can restrict the domain to [latex]80 \leq q[/latex]. (That’s good because the entire profit function is a piecewise function, but we can now look just at one of the pieces.) For [latex]q \geq 80[/latex], the daily profit will be [latex]\pi (q) = ( 50-(q-80)q = 130q-q^2[/latex]. On to calculus: [latex]\pi ' (q) = 130-2q[/latex]. The only critical point is when [latex]q = 65[/latex]; this is not in the domain we’re interested in. Time to consider the endpoints: the only endpoint is [latex]q = 80[/latex], where the profit is [latex]\$4000[/latex] per day. Is this the maximum? Time to consider the geometry. Notice that the derivative is negative for all [latex]q[/latex] bigger than [latex]80[/latex], so the profit function decreases if we have more than [latex]80[/latex] seats. (You can confirm this by checking some points – with [latex]80[/latex] seats, the profit is [latex]\$4000[/latex], but with [latex]81[/latex] seats the profit drops to [latex]$3969.[/latex]) Profit is maximized when there are [latex]80[/latex] seats in the coffee shop. 86. a. The fixed cost is [latex]\$64.[/latex]. c. the average cost is [latex]AC(q) = \frac{64+1.5q+0.1q^2}{q} = \frac{64}{q} + 1.5 + 0.01q.[/latex]. d. To minimize average cost; use calculus: [latex]AC'(q) =- \frac{64}{q^2}+0.01[/latex]. [latex]AC[/latex] has critical points at [latex]q = 0[/latex] (where the average cost is also undefined) and at [latex]q = 80[/latex]. [latex]AC' ' (80) > 0[/latex], so the critical points are a minimum. The average cost is minimized when Alicia makes [latex]80[/latex] oven mitts.
88.
[latex]g(220 \approx g(20) + g'(20)(22-30) = 35 - 4 = 31[/latex].
90.
The function we want to estimate values of is [latex]f(x) = \sqrt[3]{x}[/latex]. We want to estimate the value of the function at [latex]x = 9[/latex]. We know the value of the function at [latex]8,[/latex] so we’ll use [latex]a = 8[/latex]. TLA says, [latex]f(x) \approx f(a) + f'(a)(x-a)[/latex]). We know that [latex]f(8) = 2[/latex]. We also know [latex]f'(8) = \frac{1}{3} (8) ^{\frac{-2}{3}}= \frac{1}{12}.[/latex]. We estimate that [latex]f(9) = 2 + \frac{1}{12}(9-8) = \frac{25}{12} \approx 2.083[/latex] . (My calculator tells me that the cube root of [latex]9[/latex] is about [latex]2.080[/latex], so we are pretty close.)
92.
Elasticity is given by [latex]E = | \frac{p}{q}* \frac{dp}{dq} |[/latex], so we need [latex]p, q[/latex] and the derivative. The price is given by [latex]p = 7.5[/latex]. We can find q from the demand function; when [latex]p = 7.5, q = 20[/latex]. Finally, the derivative [latex]\frac{dp}{dq} = -8[/latex]. So [latex]E = | \frac{p}{q}* \frac{dp}{dq} | = | \frac{7.5}{20} * (-8) | = 3 > 1[/latex]. Demand is elastic; if she increases her price, her revenue will go down. In fact, if she were to decrease her price, her revenue would increase.
Media Attributions
- chapter2_solutions_63_1
- chapter2_solutions_63_2
- chapter2_solutions_63_4

