Chapter 2: Limits and The Derivative
Chapter 2 Review Exercises: Limits
From Calculus, Volume 1, by Strang and Herman, OpenStax (Web), licensed under a CC BY-NC-SA 4.0 License.
True or false?
1. A function has to be continuous at [latex]x=a[/latex] if the [latex]\underset{x\to a}{\lim}f(x)[/latex] exists.
2. You can use the quotient rule to evaluate [latex]\underset{x\to 0}{\lim}\frac{\sin x}{x}[/latex].
Solution
False
3. If there is a vertical asymptote at [latex]x=a[/latex] for the function [latex]f(x)[/latex], then [latex]f[/latex] is undefined at the point [latex]x=a[/latex].
4. If [latex]\underset{x\to a}{\lim}f(x)[/latex] does not exist, then [latex]f[/latex] is undefined at the point [latex]x=a[/latex].
Solution
False. A removable discontinuity is possible.
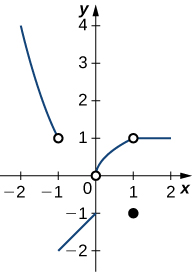
5. Using the graph of [latex]f(x)[/latex], find each of the following or explain why it does not exist.
- [latex]\underset{x\to -1^-}{\lim}f(x)[/latex]
- [latex]\underset{x\to -1^+}{\lim}f(x)[/latex]
- [latex]\underset{x\to -1}{\lim}f(x)[/latex]
- [latex]\underset{x\to 1}{\lim}f(x)[/latex]
- [latex]f(1)[/latex]
- [latex]\underset{x\to 0^+}{\lim}f(x)[/latex]
- [latex]\underset{x\to 0^-}{\lim}f(x)[/latex]
- [latex]\underset{x\to 0}{\lim}f(x)[/latex]
- [latex]\underset{x\to 2}{\lim}f(x)[/latex]
In the following exercises, evaluate the limit algebraically or explain why the limit does not exist (DNE).
6. [latex]\underset{x\to 2}{\lim}\frac{2x^2-3x-2}{x-2}[/latex]
Solution
5
7. [latex]\underset{x\to 0}{\lim}3x^2-2x+4[/latex]
8. [latex]\underset{x\to 3}{\lim}\frac{x^3-2x^2-1}{3x-2}[/latex]
Solution
[latex]8/7[/latex]
9. [latex]\underset{x\to -5}{\lim}\frac{x^2+25}{x+5}[/latex]
Solution
DNE
10. [latex]\underset{x\to 2}{\lim}\frac{3x^2-2x-8}{x^2-4}[/latex]
11. [latex]\underset{x\to 1}{\lim}\frac{x^2-1}{x^3-1}[/latex]
Solution
[latex]2/3[/latex]
12. [latex]\underset{x\to 1}{\lim}\frac{x^2-1}{\sqrt{x}-1}[/latex]
13. [latex]\underset{x\to 4}{\lim}\frac{4-x}{\sqrt{x}-2}[/latex]
Solution
−4
14. [latex]\underset{x\to 4}{\lim}\frac{1}{\sqrt{x}-2}[/latex]
15. [latex]\underset{x\to 2^-}{\lim}\frac{\frac{1}{2}-\frac{1}{x}}{(x-2)^2}[/latex]
Solution
[latex]−\infty[/latex]
16. [latex]\underset{x\to 1^-}{\lim}\frac{|x-1|}{x^2-1}[/latex]
17. [latex]\underset{t\to 5}{\lim}\frac{t-5}{\sqrt{t-4}-1}[/latex]
Solution
2
18. [latex]\underset{x\to2}{\lim}\frac{x^2+x-6}{4-x^2}[/latex]
19. [latex]\underset{x\to 4}{\lim}\frac{\sqrt{8-x}-2}{4-x}[/latex]
Solution
[latex]\frac{1}{4}[/latex]
20. [latex]\underset{x\to 0}{\lim}\frac{\frac{1}{x+7}-\frac{1}{7}}{x}[/latex]
21. [latex]\underset{x\to -4^-}{\lim}\frac{\frac{1}{4} + \frac{1}{x}}{x+4}[/latex]
Solution
[latex]-\frac{1}{16}[/latex]
22. [latex]\underset{x\to 7^-}{\lim}\frac{-1}{(x-7)^{2021}}[/latex]
23. [latex]\underset{x\to -6^-}{\lim}\frac{2x+12}{|x+6|}[/latex]
Solution
[latex]-2[/latex]
24. [latex]\underset{x\to -6}{\lim}\frac{2x+12}{|x+6|}[/latex]
In the following exercises, evaluate the limits to infinity.
25. [latex]\underset{x\to -\infty}{\lim}\frac{\sqrt{11x^2+4x}}{5-4x}[/latex]
Solution
[latex]\frac{\sqrt{11}}{4}[/latex]
26. [latex]\underset{x\to -\infty}{\lim}\frac{\sqrt{7x^2-4x}}{2x-3}[/latex]
27. [latex]\underset{x\to \infty}{\lim}(x-\sqrt{x+1})[/latex]
Solution
[latex]\infty[/latex]
28. [latex]\underset{x\to \infty}{\lim}\sqrt{\frac{3x^2-1}{x+9x^2}}[/latex]
29. [latex]\underset{x\to \infty}{\lim}\sqrt{\frac{4x^2-1}{x+3x^2}}[/latex]
Solution
[latex]\frac{2}{\sqrt{3}}[/latex]
30. [latex]\underset{x\to -\infty}{\lim}\frac{3-x^2}{\sqrt[4]{x^8-4}}[/latex]
In the following exercises, determine the value of [latex]c[/latex] such that the function is continuous for the given value of [latex]x[/latex].
31. [latex]f(x)=\begin{cases} x^2+1 & \text{if} \, x < c \\ 2x & \text{if} \, x \le c \end{cases}[/latex]
32. [latex]f(x)=\begin{cases} \sqrt{x+1} & \text{if} \, x < -1 \\ x^2+c & \text{if} \, x \le -1 \end{cases}[/latex]
Solution
[latex]c=-1[/latex]
33. [latex]f(x)=\begin{cases} \frac{c^2}{3} (x+3) & \text{if} \, x < 0 \\ c+2 & \text{if} \, x = 0 \\ \frac{2}{3}(cx)^2 +1 & \text{if} \, x > 0 \end{cases}[/latex]
34. [latex]f(x)=\begin{cases} x+c & \text{if} \, x \le 3 \\ \frac{1}{x} & \text{if} \, x > 3\end{cases}[/latex]
Solution
[latex]c=-\frac{8}{3}[/latex]
In the following exercises, determine all horizontal and vertical asymptotes.
35. [latex]f(x) = \frac{3x^2-1}{2x^2+7x-4}[/latex]
36. [latex]f(x) = \frac{4x^3 -2x}{x^3-1}[/latex]
Solution
Horizontal: [latex]y=4[/latex]; Vertical: [latex]x = 1[/latex]
37. [latex]f(x) = \frac{\sqrt{2x^2+3}}{x^2-2x-3}[/latex]
37. [latex]f(x) = \frac{2x^2-1}{\sqrt{5x^4+2}}[/latex]
Solution
Horizontal: [latex]y=\frac{2}{\sqrt{5}}[/latex]; Vertical: none
In the following exercises, use the intermediate value theorem (IVT) to show that the given functions have an x-intercept in the given interval.
39. [latex]x^8 - 4x^3 = x + 1[/latex] on the interval [latex][-1,1][/latex]
40. [latex]f(x) =\frac{3}{x^4} -x^2+2[/latex] on the interval [latex][-2,-1][/latex]
Solution
Since [latex]f(x)[/latex] is continuous on [-2,-1] and [latex]f(-2) < 0[/latex] and [latex]f(-1) > 0[/latex], then by IVT, there exists a root on the given interval.
41. A ball is thrown into the air and the vertical position is given by [latex]x(t)=-4.9t^2+25t+5[/latex]. Use the intermediate value theorem to show that the ball must land on the ground sometime between 5 sec and 6 sec after the throw.
42. A particle moving along a line has a displacement according to the function [latex]x(t)=t^2-2t+4[/latex], where [latex]x[/latex] is measured in meters and [latex]t[/latex] is measured in seconds. Find the average velocity over the time period [latex]t=[0,2][/latex].
Solution
[latex]0[/latex] m/sec
In the following exercises, use the precise definition of limit to prove the limit.
43. [latex]\underset{x\to 1}{\lim}(8x+16)=24[/latex]
44. [latex]\underset{x\to 0}{\lim}x^3=0[/latex]
Solution
[latex]\delta =\sqrt[3]{\epsilon}[/latex]
Media Attributions
- CNX_Calc_Figure_02_05_207

