Chapter 2 Matrices

2.1 Systems of Equations

Learning Objectives

By the end of this section, you will be able to:

  • Solve linear systems using graphing
  • Solve linear systems using substitution
  • Solve linear systems using elimination (addition)
  • Classify systems as independent, inconsistent, or dependent
  • Solve linear systems in 3 variables

Back when studying linear equations, we found the intersection of two lines. Doing so allowed us to solve interesting problems by finding a pair of values that satisfied two different equations. While we didn’t call it this at the time, we were solving a system of equations.

A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously.

A solution to a system is a set of numerical values for each variable in the system that will satisfy all equations in the system at the same time.

Not every system will have exactly one solution, but we’ll look more closely at that later.

To check to see if an ordered pair is a solution to a system of equations, you would:

  1. Substitute the ordered pair into each equation in the system.
  2. Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.

Example 1

Determine whether the ordered pair [latex](5, 1)[/latex] is a solution to the given system of equations.

[latex]\begin{cases} x+3y=8\\2x-9=y\end{cases}[/latex]

Substitute the ordered pair [latex](5, 1)[/latex] into both equations.

[latex]\begin{array}{rclr} (5)+3(1) & = & 8 \\ 8 & = & 8& \text{True}\\ \\2(5)-9 &=&(1)\\1&=&1&\text{True}\end{array}[/latex]

The ordered pair [latex](5, 1)[/latex] satisfies both equations, so it is the solution to the system.

Solving a System by Graphing

There are three common methods for solving systems of linear equations with two variables. The first is solving by graphing.

To solve a system using the graphing method, you would:

  1. Graph both equations
  2. The solution to the system is the intersection of the lines.

Example 2

Solve the following system of equations by graphing.

[latex]\begin {cases} 2x+y=-8\\x-y=-1\end {cases}[/latex]

Solve the first equation for [latex]y.[/latex]

[latex]\begin{array}{rcl}2x+y&=&-8\\y&=&-2x-8&\end{array}[/latex]

Solve the second equation for [latex]y.[/latex]

[latex]\begin{array}{rcl}x-y&=&-1\\y&=&x+1\end{array}[/latex]

Graph both equations on the same set of axes.

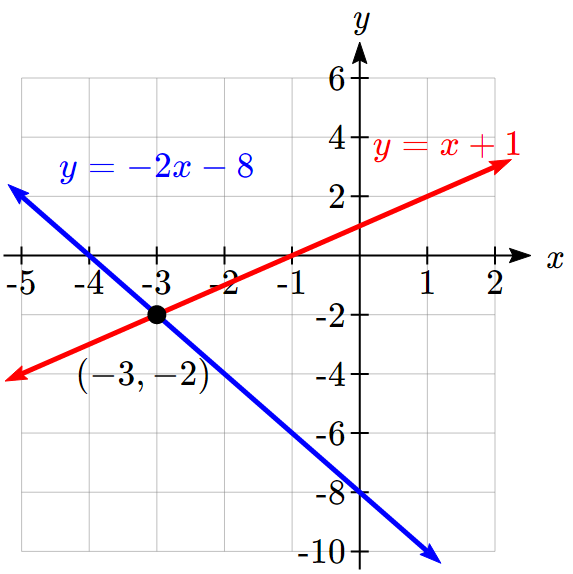
This image shows two lines that intersect at the point negative three comma negative 2. The red line angles upward from the third quandrant into the first quadrant. The blue line angles downward from the second quadrant into the fourth quadrant.
Figure 1. Graph of intersecting lines

The lines appear to intersect at the point [latex](-3, -2).[/latex]

We can check to make sure that this is the solution to the system by substituting the ordered pair into both equations.

[latex]\begin{array}{rclr}2(-3)+(-2) & = & -8 \\ -8 & = & -8 &\text{True}\\ \\(-3)-(-2) & =&-1\\-1&=&-1&\text{True}\end{array}[/latex]

The solution to the system is the ordered pair [latex](-3, -2)[/latex].

Exercise 1

While this method can work well enough when the solution values are both integers, it is not very useful when the intersection is not at a clear point. Additionally, it requires solving both equations for y, which adds extra steps. Because of these limitations, solving by graphing is rarely used, but can be useful for checking whether your algebraic answers are reasonable.

Solving a System by Substitution

Another method for solving a system of equations is the substitution method, in which we solve one of the equations for one variable and then substitute the result into the second equation to solve for the second variable.

To solve a system using substitution, you would:

  1. Solve one of the two equations for one of the variables in terms of the other.
  2. Substitute the expression for this variable into the second equation, then solve for the remaining variable.
  3. Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
  4. Check the solution in both equations.

Example 3

Solve the following system of equations by substitution.

[latex]\begin {cases} -x+y=-5\\ 2x-5y=1\end {cases}[/latex]

First, we will solve the first equation for [latex]y[/latex].

[latex]\begin {array}{rcl}-x+y&=&-5\\ y& =&x-5\end{array}[/latex]

Now we can substitute the expression [latex]x-5[/latex] for [latex]y[/latex] in the second equation.

[latex]\begin {array}{rcl}2x-5y&=&1\\2x-5(x-5)&=&1\\2x-5x+25&=&1\\-3x&=&-24\\x&=&8\end{array}[/latex]

Now, we substitute [latex]x=8[/latex] into the first equation and solve for [latex]y[/latex].

[latex]\begin{array}{rcl}-(8)+y&=&-5\\y&=&3\end{array}[/latex]

Our solution is [latex](8, 3)[/latex].

We can check the solution by substituting [latex](8, 3)[/latex] into both equations.

[latex]\begin{array}{rclr}-x+y&=&-5\\-(8)+(3)&=&-5&\text{True}\\ \\2x-5y&=&1\\2(8)-5(3)&=&1&\text{True}\end{array}[/latex]

Exercise 2

Substitution can always be used, but is an especially good choice when one of the variables in one of the equations has a coefficient of 1 or -1, making it easy to solve for that variable without introducing fractions. This is fairly common in many applications.

Example 4

Julia has just retired, and has $600,000 in her retirement account that she needs to reallocate to produce income. She is looking at two investments: a very safe guaranteed annuity that will provide 3% interest, and a somewhat riskier bond fund that averages 7% interest. She would like to invest as little as possible in the riskier bond fund, but needs to produce $40,000 a year in interest to live on. How much should she invest in each account?

Notice there are two unknowns in this problem: the amount she should invest in the annuity and the amount she should invest in the bond fund. We can start by defining variables for the unknowns:

[latex]a:[/latex] The amount (in dollars) she invests in the annuity

[latex]b:[/latex] The amount (in dollars) she invests in the bond fund.

Our first equation comes from noting that together she is going to invest $600,000: [latex]a+b=600,000[/latex]

Our second equation will come from the interest. She earns 3% on the annuity, so the interest earned in a year would be [latex]0.03a.[/latex] Likewise, the interest earned on the bond fund in a year would be [latex]0.07b.[/latex] Together, these need to total $40,000, giving the equation: [latex]0.03a+0.07b=40,000[/latex]

Together, these two equations form our system. The first equation is an ideal candidate for the first step of substitution – we can easily solve the equation for [latex]a[/latex] or [latex]b:[/latex] [latex]a=600,000-b[/latex]

Then we can substitute this expression for [latex]a[/latex] in the second equation and solve.

[latex]\begin {array}{rcl}0.03(600,000-b)+0.07b&=&40,000\\18,000-0.03b+0.07b&=&40,000\\0.04b&=&22,000\\b&=&550,000\end {array}[/latex]

Now substitute this back into the equation [latex]a=600,000-b[/latex] to find [latex]a[/latex].

[latex]\begin{array}{rcl}a&=&600,000-550,000\\a&=&50,000\end{array}[/latex]

In order to reach her goal, Julia will have to invest $550,000 in the bond fund, and $50,000 in the annuity.

Solving a System by the Addition Method

A third method of solving systems of linear equations is the addition method, also called the elimination method. In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.

To solve with the addition (or elimination) method, you would:

  1. Write both equations with [latex]x-[/latex] and [latex]y-[/latex]variables on the left side of the equal sign and constants on the right.
  2. Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
  3. Solve the resulting equation for the remaining variable.
  4. Substitute that value into one of the original equations, and solve for the second variable.
  5. Check the solution by substituting the values into the other equation.

Often using the addition method will require multiplying one or both equations by a constant so terms will eliminate.

Example 5

Solve the following system by elimination.

[latex]\begin{cases}20b+30p=3900\\15b+30p=3300\end{cases}[/latex]

Adding the equations would not eliminate a variable, but we notice that the coefficients on [latex]p[/latex] are the same, so multiplying one of the equations by -1 will change the sign of the coefficients. Multiplying the second equation by -1 gives the system

[latex]\begin{array}{rcl}20b+30p&=&3900\\-15b-30p&=&-3300\end{array}[/latex]

Adding these equations gives

[latex]\begin{array}{rcl}5b&=&600\\b&=&120\end{array}[/latex]

Substituting [latex]b = 30[/latex] into the first equation,

[latex]\begin{array}{rcl}20(120)+30p&=&3900\\2400+30p&=&3900\\30p&=&1500\\p&=&50\end{array}[/latex]

The solution is [latex]b = 120[/latex], [latex]p = 50[/latex].

Checking our answer in the second equation:

[latex]\begin{array}{rcl}15(120)+30(50)&=&3300\\1800+1500&=&3300\\3300&=&3300\end{array}[/latex]

Exercise 3

Example 6

Solve the given system of equations in two variables by addition.

[latex]\begin{cases}2x+3y=-16\\5x+10y=30\end{cases}[/latex]

One equation has [latex]2x[/latex] and the other has [latex]5x[/latex]. The least common multiple is [latex]10x[/latex] so we will have to multiply both equations by a constant in order to eliminate one variable. Let’s eliminate [latex]x[/latex] by multiplying the first equation by [latex]-5[/latex] and the second equation by [latex]2[/latex].

[latex]\begin{array}{rcl}-5(2x+3y)&=&-5(-16)\\-10x-15y&=&80\\2(5x-10y)&=&2(30)\\10x-20y&=&60\end{array}[/latex]

Then, we add the two equations together.

[latex]\begin{array}{rcl}-10x-15y&=&80\\10x-20y&=&60\\ \hline-35y&=&140\\y&=&-4\end{array}[/latex]

Substitute [latex]y=-4[/latex] into the original first equation.

[latex]\begin{array}{rcl}2x+3(-4)&=&-16\\2x-12&=&-16\\2x&=&-4\\x&=&-2\end{array}[/latex]

The solution is [latex](-2, -4)[/latex]. Check it in the other equation.

[latex]\begin{array}{rcl}5x-10y&=&30\\5(-2)-10(-4)&=&30\\-10+40&=&30\\30&=&30\end{array}[/latex]

Exercise 4

Dependent and Inconsistent Systems

Up until now, we have only considered cases where there is exactly one solution to the system. We can categorize systems of linear equations by the number of solutions. A consistent system of equations has at least one solution. A consistent system is considered to be an independent system if it has a single solution, such as the examples we just explored. The two lines have different slopes and intersect at one point in the plane.

A consistent system is considered to be a dependent system if the equations have the same slope and the same y-intercepts. In other words, the lines coincide so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions.

Another type of system of linear equations is an inconsistent system, which is one in which the equations represent two parallel lines. The lines have the same slope and different y-intercepts. There are no points common to both lines; hence, there is no solution to the system.

Types of Linear Systems

  • An independent system has exactly one solution pair. The point where the two lines intersect is the only solution.
  • An inconsistent system has no solution. Notice that the two lines are parallel and will never intersect.
  • A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.

Independent System

 

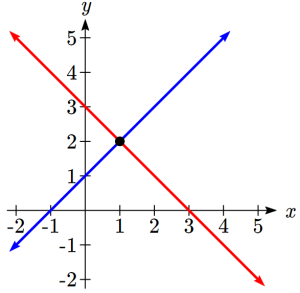Graph of two lines intersecting at one point
Figure 2. Intersecting lines

Inconsistent System

 

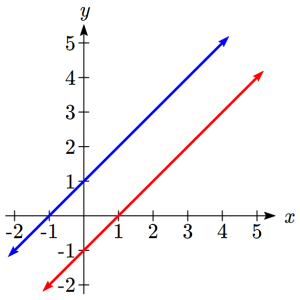Graph showing two lines that do not intersect
Figure 3. Parallel lines

Dependent System

 

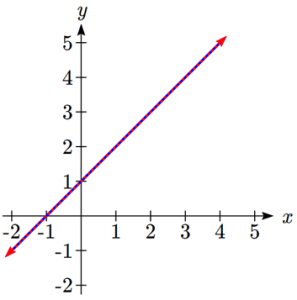Graph showing two lines one on top of the other
Figure 4. Coincident lines

We can use substitution or addition to identify inconsistent systems. Recall that an inconsistent system consists of parallel lines that have the same slope but different y-intercepts. They will never intersect. When searching for a solution to an inconsistent system, we will come up with a false statement, such as [latex]12=0[/latex].

Example 7

Solve the following system of equations.

[latex]\begin{cases}x=9-2y\\x+2y=13\end{cases}[/latex]

We can approach this problem in two ways. Because one equation is already solved for [latex]x[/latex] the most obvious step is to use substitution.

[latex]\begin{array}{rcl}x+2y&=&13\\(9-2y)+2y&=&13\\9+0y&=&13\\9&=&13\end{array}[/latex]

Clearly, this statement is a contradiction (a false statement) because [latex]9\neq13[/latex] Therefore, the system has no solution, and the system is inconsistent.

Recall that a dependent system of equations in two variables is a system in which the two equations represent the same line. Dependent systems have an infinite number of solutions because all of the points on one line are also on the other line. After using substitution or addition, the resulting equation will be an identity, such as [latex]0=0[/latex].

Example 8

Find a solution to the system of equations using the addition method.

[latex]\begin{cases}x+3y=2\\3x+9y=6\end{cases}[/latex]

 With the addition method, we want to eliminate one of the variables by adding the equations. In this case, let’s focus on eliminating [latex]x[/latex]. If we multiply both sides of the first equation by -3 then we will be able to eliminate the x-variable.

[latex]\begin{array}{rclc}x+3y&=&2\\(-3)(x+3y)&=&(-3)(2)&\text{Multiply both sides of the equation by -3.}\\-3x-9y&=&-6\end {array}[/latex]

Now add the equations together to eliminate the [latex]x[/latex] variable.

[latex]\begin{array}{rcl}-3x-9y&=&-6\\3x+9y&=&6\\ \hline 0&=&0\end{array}[/latex]

We can see that there will be an infinite number of solutions that satisfy both equations. In some cases, realizing there are an infinite number of solutions is enough, and we can stop there. In other cases, we will want to describe the set of solutions.

One way is to simply say it’s the set of points that satisfy [latex]x+3y=2[/latex] , but often we would solve that equation for [latex]y[/latex] and describe the solution as the set of points [latex](x, -\frac{1}{3}x+\frac{2}{3})[/latex]

Exercise 5

Solve the following systems of equations.

a) [latex]\begin{cases}2y-2x=2\\2y-2x=6\end{cases}[/latex]

Solution

No solution. The system is inconsistent.

 

b) [latex]\begin{cases}y-2x=5\\-3y+6x=-15\end{cases}[/latex]

Solution

The system is dependent, so there are infinite solutions of the form [latex](x, 2x+5)[/latex]

Systems with 3 variables in 3 unknowns

In systems of two variables, a solution was an ordered pair [latex](x, y)[/latex] that satisfied both equations. The solution set to a three-by-three system is an ordered triple. Graphically, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.

Example 9

Determine whether the ordered triple [latex](3, -2, 1)[/latex] is a solution to the system.

[latex]\begin{array}{rclc}x+y+z&=&2&(1)\\6x-4y+5z&=&31&(2)\\5x+2y+2z&=&13&(3)\end{array}[/latex]

We will check each equation by substituting in the values of the ordered triple for [latex]x[/latex], [latex]y[/latex], and [latex]z[/latex].

Equation (1):

[latex]\begin{array}{rclc}x+y+z&=&2\\(3)+(-2)+(1)&=&2&\text{True}\end{array}[/latex]

Equation (2):

[latex]\begin{array}{rclc}6x-4y+5z&=&31\\ 6(3)-4(-2)+5(1)&=&31\\ 18+8+5&=&31&\text{True}\end{array}[/latex]

Equation (3):

[latex]\begin{array}{rclc}5x+2y+2z&=&13\\ 5(3)-2(-2)+2(1)&=&13\\15-4+2&=&13&\text{True}\end{array}[/latex]

The ordered triple [latex](3, -2, 1)[/latex] is indeed a solution to the system.

We can utilize the techniques we learned in the last section to solve 3-by-3 systems of equations by reducing the problem to one we already know how to solve.

  1. Given a linear system of three equations, solve for three unknowns
  2. Pick any pair of equations and solve for one variable.
  3. Pick another pair of equations and solve for the same variable.
  4. You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
  5. Back-substitute known variables into any one of the original equations and solve for the missing variable.

Example 10

Find a solution to the following system. The equations are numbered so we can refer to them more easily.

[latex]\begin{cases} x-2y+3z=9 \text{ } (1)\\-x+3y-z=-6 \text{ } (2)\\2x-5y+5z=17 \text{ } (3)\end{cases}[/latex]

There will always be several choices as to where to begin, but the most obvious first step here is to eliminate [latex]x[/latex] by adding equations (1) and (2).

[latex]\begin{array}{rclc}x-2y+3z&=&9&(1)\\-x+3y-z&=&-6&(2)\\ \hline y+2z&=&3&(4)\end{array}[/latex]

The second step is multiplying equation (1) by -2 and adding the result to equation (3). These two steps will eliminate the variable [latex]x[/latex].

[latex]\begin{array}{rclcc}-2x+4y-6z&=&-18&(1)&\text{multiplied by -2}\\2x-5y+5z&=&17&(3)\\ \hline -y-z&=&-1&(5)\end{array}[/latex]

In equations (4) and (5), we have created a new two-by-two system. We can solve for [latex]z[/latex] by adding the two equations.

[latex]\begin{array}{rclc}y+2z&=&3&(4)\\-y-z&=&-1&(5)\\ \hline z&=&2&(6)\end{array}[/latex]

Choosing one equation from each new system, we obtain the upper triangular form:

[latex]\begin{array}{rclc}x-2y+3z&=&9&(1)\\y+2z&=&3&(4)\\z&=&2&(6)\end{array}[/latex]

Next, we back-substitute [latex]z=2[/latex] into equation (4) and solve for [latex]y[/latex].

[latex]\begin{array}{rcl}y+2(2)&=&3\\y+4&=&3\\y&=&-1\end{array}[/latex]

Finally, we can back-substitute [latex]z=2[/latex] and [latex]y=-1[/latex] into equation (1). This will yield the solution for

[latex]\begin{array}{rcl}x-2(-1)+3(2)&=&9\\x+2+6&=&9\\x&=&1\end{array}[/latex]

The solution is the ordered triple [latex](1, -1, 2)[/latex].

Exercise 6

Many problems in real life depend on more than two unknowns.

Example 11

Chad is trying to plan a meal to meet specific nutritional goals. He wants to construct a dish containing rice, tofu, and peanuts that will provide 30g of protein, 14g of fat, and 50g of carbohydrates. How much of each ingredient should he use?

First off, we’re assuming any other ingredients used in the recipe aren’t contributing significantly enough to the nutrition to be considered. To answer this question, we’ll first need to know the nutritional content for the ingredients. Looking these up:

White rice: 1 cup provides: 0g fat, 44g carbohydrates, 4g protein

Tofu: 1 cup provides: 10g fat, 5g carbohydrates, 20g protein

Peanuts: 1 cup provides: 72g fat, 31g carbohydrates, 35g protein

Now we can define our variables. We are interested in the amount of each ingredient to use, so we’ll define our variables as the quantity of each ingredient:

[latex]r[/latex]: cups of rice, [latex]t[/latex]: cups of tofu, [latex]p[/latex]: cups of peanuts.

Now for each nutrient, we can create an equation. Since 1 cup of rice provides [latex]44g[/latex] carbohydrates, [latex]r[/latex] cups will provide [latex]44r[/latex] grams of carbohydrates. Likewise [latex]t[/latex] cups of tofu will provide [latex]5t[/latex] grams, and [latex]p[/latex] cups of peanuts will provide [latex]31p[/latex] grams. Together we want our recipe to provide [latex]50g[/latex] of carbohydrates, giving the equation:

[latex]44r+5t+31p=50[/latex]

Doing the same for fat and protein gives the full system:

[latex]\begin{cases}44r+5t+31p=50\\10t+72p=14\\4r+20t+35p=30\end{cases}[/latex]

Now we can solve the system.

Step 1. Notice that the section equation already does not involve the variable [latex]r[/latex]. To make things simpler, a first step might be to interchange the last two equations so the two equations with three variables will line up.

[latex]\begin{array}{rclc}44r+5t+31p&=&50&(1)\\4r+20t+35p&=&30&(2)\\10t+72p&=&14&(3)\end{array}[/latex]

Step 2. Since [latex]r[/latex] is already eliminated in the last equation, we’ll eliminate [latex]r[/latex] from the first two equations. Multiply equation (2) by -11

[latex]\begin{array}{rclc}44r+5t+31p&=&50&(1)\\-44r-220t-385p&=&-330&(2)\\10t+72p&=&14&(3)\end{array}[/latex]

Step 3. Add equations (1) and (2), writing the result as row 2.

[latex]\begin{array}{rclc}44r+5t+31p&=&50&(1)\\-215t-354p&=&-280&(2)\\10t+72p&=&14&(3)\end{array}[/latex]

Step 4. Multiply equation (2) by 2 and equation (3) by 43

[latex]\begin{array}{rclc}44r+5t+31p&=&50&(1)\\-430t-708p&=&-560&(2)\\430t+3096p&=&602&(3)\end{array}[/latex]

Step 5. Add equations (2) and (3), writing the result in row 3

[latex]\begin{array}{rclc}44r+5t+31p&=&50&(1)\\-430t-708p&=&-560&(2)\\2388p&=&42&(3)\end{array}[/latex]

Step 6. Solve for [latex]p[/latex] in equation 3. For a real life problem like this, decimal approximations are probably fine.

[latex]\begin{array}{rcl}2388p&=&42\\p&=&\frac{42}{2388}\approx{0.0176}\end{array}[/latex]

Step 7. Back substitute the value for [latex]p[/latex] into equation (2) to solve for [latex]t[/latex].

[latex]\begin{array}{rcl}-430t-708(0.0176)&=&-560\\-430t-12.4608&=&-560\\-430t&=&-547.5392\\t&=&\frac{-547.5392}{-430}\approx{1.273}\end{array}[/latex]

Step 8. Back substitute the values for [latex]p[/latex] and [latex]t[/latex] into equation (1) and solve for [latex]r[/latex].

[latex]\begin{array}{rcl}44r+5(1.273)+31(0.0176)&=&50\\44r&=&43.0894\\r&\approx{ }&0.979\end{array}[/latex]

To meet his nutritional goals, Chad should use 0.979 cups of rice, 1.273 cups of tofu, and 0.0176 cups of peanuts.

This particular system was rather unpleasant to solve. In the rest of the chapter we will learn some other techniques for solving complex systems.

Media Attributions

definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Finite Mathematics Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book