5.5 Set Operations with Three Sets

Ashley Segalla; Kiel Ellis; Renae Broussard; Toni Spahn

Chapter 5 Sets

5.5 Set Operations with Three Sets

Learning Objectives

By the end of this section, you will be able to:

Interpret Venn diagrams with three sets.
Create Venn diagrams with three sets.
Apply set operations to three sets.
Prove equality of sets using Venn diagrams.

Have you ever searched for something on the Internet and then soon after started seeing multiple advertisements for that item while browsing other web pages? Large corporations have built their business on data collection and analysis. As we start working with larger data sets, the analysis becomes more complex. In this section, we will extend our knowledge of set relationships by including a third set.

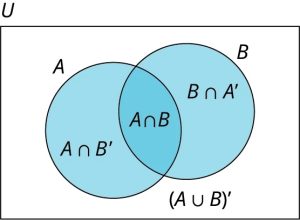
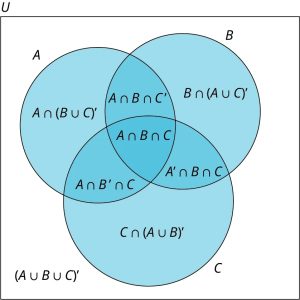
A Venn diagram with two intersecting sets breaks up the universal set into four regions; simply adding one additional set will increase the number of regions to eight, doubling the complexity of the problem.

Venn Diagrams with Three Sets

Below is a Venn diagram with two intersecting sets, which breaks the universal set up into four distinct regions.

A two-set Venn diagram of A and B intersecting one another is given. Set A shows A union of B complement. Set B shows B union of A complement. The intersection of the sets shows A union B. Outside the set, the complement of A union B is given. Outside the Venn diagram, it is marked U. — Figure 1. Venn diagram with two intersecting sets

Next, we see a Venn diagram with three intersecting sets, which breaks up the universal set into eight distinct regions.

A three-set Venn diagram of A, B, and C intersecting one another is given. Set A shows A union of the complement of (B union C). Set B shows B union of the complement of (A union C). Set C shows the C union of the complement of (A union B). The intersection of sets A and B shows A union B union complement of C. The intersection of sets B and C shows the complement of A union B union C. The intersection of sets A and C show the A union complement of B union C. The intersection of the sets shows A union B union C. Outside the set, the complement of (A union B union C is given). Outside the Venn diagram, it is marked U. — Figure 2. Three set Venn diagram

In the next example, we will explore the three main blood factors, [latex]A, B[/latex] and [latex]Rh[/latex]. The following background information about blood types will help explain the relationships between the sets of blood factors. If an individual has blood factor [latex]A[/latex] or [latex]B[/latex], those will be included in their blood type. The [latex]Rh[/latex] factor is indicated with a [latex]+[/latex] or a [latex]-[/latex]. For example, if a person has all three blood factors, then their blood type would be [latex]AB^+[/latex]. In the Venn diagram, they would be in the intersection of all three sets, [latex]A \cap B \cap Rh^+[/latex]

A \cap B \cap R h^{+} .

If a person did not have any of these three blood factors, then their blood type would be [latex]O^-[/latex]

O^{-},

and they would be in the set [latex](A \cup B \cup Rh^+)'[/latex] which is the region outside all three circles.

Example 1

Use the Venn diagram below, which shows the blood types of [latex]100[/latex] people who donated blood at a local clinic, to answer the following questions.

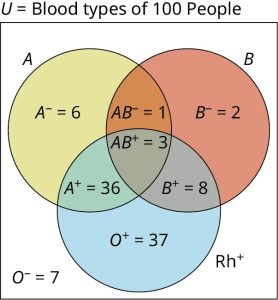
A three-set Venn diagram A, B, and Rh plus overlapping one another is given. Set A shows A dash equals 6. Set B shows B dash equals 2. Set Rh plus shows O plus dash equals 37. The intersection of sets A and B shows AB dash equals 1. The intersection of sets B and Rh plus shows B plus equals 8. The intersection of sets A and Rh plus shows A plus equals 36. The intersection of all three sets shows AB plus equals 3. Outside the set, 'O dash equals 7' is given. Outside the Venn diagram, it is marked 'U equals Blood types of 100 people.' — Figure 3. Blood types of 100 people Venn diagram

a) How many people with a type [latex]A[/latex] blood factor donated blood?

The number of people who donated blood with a type [latex]A[/latex] blood factor will include the sum of all the values included in the [latex]A[/latex] circle. It will be the union of sets [latex]A^-, A^+, AB^-[/latex], and [latex]AB^+[/latex] $A^{-}, A^{+}, A B^{-} and A B^{+} .$ [latex]n(A)=n(A^-)+n(A^+)+n(AB^-)+n(AB^+)=6+36+1+3=46[/latex].

b) Julio has blood type [latex]B^+[/latex]. If he needs to have surgery that requires a blood transfusion, he can accept blood from anyone who does not have a type [latex]A[/latex] blood factor. How many people donated blood that Julio can accept?

In part a, it was determined that the number of donors with a type [latex]A[/latex] blood factor is [latex]46[/latex]. To determine the number of people who did not have a type [latex]A[/latex] blood factor, use the following property $A^{'}$ union [latex]A[/latex] is equal to [latex]U[/latex], which means [latex]n(A)+n(A')=n(U)[/latex] $n (A) + n (A^{'}) = n (U),$ and [latex]n(A')=n(U)-n(A)=100-46=54[/latex]. Thus, [latex]54[/latex] people donated blood that Julio can accept.

c) How many people who donated blood do not have the [latex]Rh^+[/latex] blood factor?

This would be everyone outside the [latex]Rh^+[/latex]circle, or everyone with a negative [latex]Rh[/latex] factor, [latex]n(Rh^-)=n(O^-)+n(A^-)+n(AB^-)+n(B^-)=7+6+1+2=16[/latex] $n (R h^{-}) = n (O^{-}) + n (A^{-}) + n (A B^{-}) + n (B^{-}) = 7 + 6 + 1 + 2 = 16.$

d) How many people had type [latex]A[/latex] and type [latex]B[/latex] blood?

To have both blood type [latex]A[/latex] and blood type [latex]B[/latex], a person would need to be in the intersection of sets [latex]A[/latex] and [latex]B[/latex]. The two circles overlap in the regions labeled [latex]AB^-[/latex] and [latex]AB^+[/latex] $A B^{+} .$ Add up the number of people in these two regions to get the total [latex]1+3=4[/latex] $1 + 3 = 4.$ This can be written symbolically as [latex]n(A \text{ and } B=A \cap B=n(AB^-)+n(AB^+)=1+3=4[/latex] $n (A and B) = n (A \cap B) = n (A B^{-}) + n (A B^{+}) = 1 + 3 = 4.$

Exercise 1

Use the same Venn diagram in the example above to answer the following questions.

a) How many people donated blood with a type B blood factor?

b) How many people who donated blood did not have a type B blood factor?

c) How many people who donated blood had a type B blood factor or were Rh⁺?

Solution

a) [latex]n(B)=n(AB^+)+n(AB^-)+n(B^+)+n(B^-)=14[/latex]

b) [latex]n(B')=n(U)-n(B)=86[/latex]

c) [latex]n(B \cup Rh^+)=87[/latex]

Creating Venn Diagrams with Three Sets

In general, when creating Venn diagrams from data involving three subsets of a universal set, the strategy is to work from the inside out. Start with the intersection of the three sets, then address the regions that involve the intersection of two sets. Next, complete the regions that involve a single set, and finally address the region in the universal set that does not intersect with any of the three sets. This method can be extended to any number of sets. The key is to start with the region involving the most overlap, working your way from the center out.

Example 2

A teacher surveyed her class of [latex]43[/latex] students to find out how they prepared for their last test. She found that [latex]24[/latex] students made flash cards, [latex]14[/latex] studied their notes, and [latex]27[/latex] completed the review assignment. Of the entire class of [latex]43[/latex] students, [latex]12[/latex] completed the review and made flash cards, [latex]9[/latex] completed the review and studied their notes, and [latex]7[/latex] made flash cards and studied their notes, while only [latex]5[/latex] students completed all three of these tasks. The remaining students did not do any of these tasks. Create a Venn diagram with subsets labeled: “Notes,” “Flash Cards,” and “Review” to represent how the students prepared for the test.

Step 1: First, draw a Venn diagram with three intersecting circles to represent the three intersecting sets: Notes, Flash Cards, and Review. Label the universal set with the cardinality of the class.

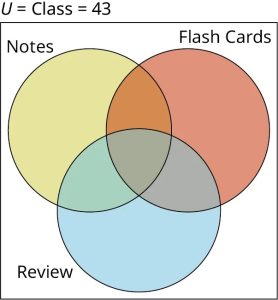
A three-set Venn diagram overlapping one another is given. The first set is labeled Notes, the second set is labeled Flash Card, and the third set is labeled Review. Outside the Venn diagram, 'U equals Class equals 43' is marked. — Figure 4. Venn diagram for Step 1

Step 2: Next, in the region where all three sets intersect, enter the number of students who completed all three tasks.

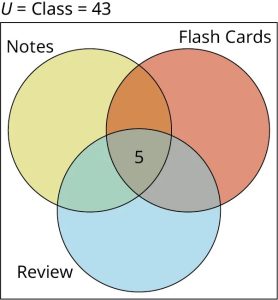
Step 3: Next, calculate the value and label the three sections where just two sets overlap.

Review and flash card overlap. A total of [latex]12[/latex] students completed the review and made flash cards, but five of these twelve students did all three tasks, so we need to subtract [latex]12-5=7[/latex]. This is the value for the region where the flash card set intersects with the review set.
Review and notes overlap. A total of [latex]9[/latex] students completed the review and studied their notes, but again, five of these nine students completed all three tasks. So, we subtract [latex]9-5=4[/latex]. This is the value for the region where the review set intersects with the notes set.
Flash card and notes overlap. A total of [latex]7[/latex] students made flash cards and studied their notes; subtracting the five students that did all three tasks from this number leaves [latex]2[/latex] students who only studied their notes and made flash cards. Add these values to the Venn diagram.

Step 4: Now, repeat this process to find the number of students who only completed one of these three tasks.

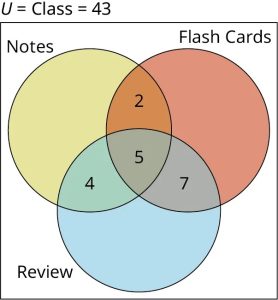
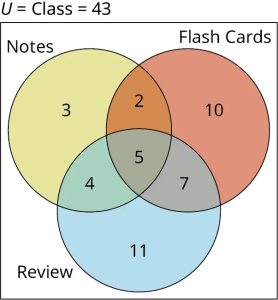
A total of [latex]24[/latex] students completed flash cards, but we have already accounted for [latex]2+5+7=14[/latex] of these. Thus, $24 - 14 = 10$ [latex] $24 - 14 = 10 "> 24 - 14 = 10$ [/latex] students who just made flash cards.
A total of [latex]14[/latex] students studied their notes, but we have already accounted for [latex]4+5+2=11[/latex] of these. Thus, [latex]14-11=3[/latex] students only studied their notes.
A total of [latex]27[/latex] students completed the review assignment, but we have already accounted for [latex]4+5+7=16[/latex] of these, which means [latex]27-16=11[/latex] students only completed the review assignment.
Add these values to the Venn diagram.

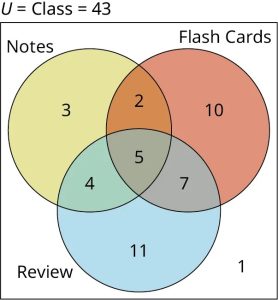
Step 5: Finally, compute how many students did not do any of these three tasks. To do this, we add together each value that we have already calculated for the separate and intersecting sections of our three sets: [latex]3+2+4+5+10+7+11=42[/latex]. Because there are [latex]43[/latex] students in the class, and [latex]43-42=1[/latex] this means only one student did not complete any of these tasks to prepare for the test. Record this value somewhere in the rectangle, but outside of all the circles, to complete the Venn diagram.

Exercise 2

A group of [latex]50[/latex] people attending a conference who preordered their lunch were able to select their choice of soup, salad, or sandwich. A total of [latex]17[/latex] people selected soup, [latex]29[/latex] people selected salad and [latex]35[/latex] people selected a sandwich. Of these orders, [latex]11[/latex] attendees selected soup and salad, [latex]10[/latex] attendees selected soup and a sandwich, and [latex]18[/latex] selected a salad and a sandwich, while [latex]8[/latex] people selected a soup, a salad, and a sandwich. Create a Venn diagram with subsets labeled “Soup,” “Salad,” and “Sandwich,” and label the cardinality of each section of the Venn diagram as indicated by the data.

Solution

A Venn diagram shows three intersecting circles inside a rectangle. The first circle representing soup is shaded in yellow and has a value of 4. The second circle representing the sandwich is shaded in red and has a value of 15. The third circle representing salad is shaded in blue and has a value of 8. The intersecting region of soup and sandwich has a value of 2. The intersecting region of soup and salad has a value of 3. The intersecting region of sandwich and salad has a value of 10. The intersecting region of all three circles has a value of 8. The rectangle represents U equals conference attendees equals 50 and has a value of 0. — Figure 9. Attendees at a conference with sets: Soup, Sandwich, Salad – Complete Venn diagram Solution

Applying Set Operations to Three Sets

Set operations are applied between two sets at a time. Parentheses indicate which operation should be performed first. As with numbers, the innermost parentheses are applied first. Next, find the complement of any sets, then perform any union or intersections that remain.

Example 3

Perform the set operations as indicated on the following sets.

[latex]U=\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\},[/latex] [latex]A= \{0, 1, 2, 3, 4, 5, 6\},[/latex] [latex]B=\{0, 2, 4, 6, 8, 10, 12\},[/latex] [latex]C=\{0, 3, 6, 9, 12\}[/latex] a) Find [latex](A \cap B)\cap C[/latex]. Parentheses first, [latex]A[/latex] intersection [latex]B[/latex] equals [latex]A \cap B=\{0, 2, 4, 6\}[/latex]

A \cap B = {0, 2, 4, 6},

the elements common to both [latex]A[/latex] and [latex]B[/latex]. [latex](A \cap B)\cap C=\{0, 2, 4, 6\} \cap \{0, 3, 6, 9, 12\}=\{0, 6\}[/latex], because the only elements that are in both sets are [latex]0[/latex] and [latex]6[/latex].

b) Find [latex]A \cap (B \cup C)[/latex] $A \cap (B \cup C) .$

Parentheses first, [latex]B[/latex] union [latex]C[/latex] equals [latex]B \cup C=\{0, 2, 3, 4, 6, 8, 9, 10, 12\}[/latex] $B \cup C = {0, 2, 3, 4, 6, 8, 9, 10, 12},$ the collection of all elements in set [latex]B[/latex] or set [latex]C[/latex] or both. [latex]A \cap (B \cup C)=\{0, 1, 2, 3, 4, 5, 6\}\cap\{0, 2, 3, 4, 6, 8, 9, 10, 12\}=\{0, 2, 3, 4, 6\}[/latex]because the intersection of these two sets is the set of elements that are common to both sets.

c) Find [latex](A \cap B) \cup C'[/latex] $(A \cap B) \cup C^{'} .$

Parentheses first, [latex]A[/latex] intersection [latex]B[/latex] equals [latex]A \cap B=\{0, 2, 4, 6\}[/latex] $A \cap B = {0, 2, 4, 6} .$ Next, find [latex]C'[/latex] $C^{'} .$ The complement of set [latex]C[/latex] is the set of elements in the universal set [latex]U[/latex] that are not in set [latex]C[/latex] $C .$ [latex]C'=\{1, 2, 4, 5, 7, 8, 10, 11\}[/latex]. Finally, find [latex](A \cap B)\cup C'=\{0, 2, 4, 6\}\cup\{1, 2, 4, 5, 7, 8, 10, 11\}=\{0, 1, 2, 4, 5, 6, 7, 8, 10, 11\}[/latex].

Exercise 3

Using the same sets from Example 3, perform the set operations indicated.

a) Find [latex]A\cap(B\cap C)[/latex].

b) Find [latex](A \cap B)\cup (A\cap C)[/latex].

c) Find [latex](A\cup C')\cap(B\cup C')[/latex].

Solution

a) [latex]A\cap (B\cap C)=\{0, 1, 2, 3, 4, 5, 6\}\cap\{0, 6, 12\}=\{0, 6\}[/latex]

b) [latex](A\cap B)\cup(B \cap C)=\{0, 2, 4, 6\}\cup \{0, 6, 12\}=\{0, 2, 4, 6, 12\}[/latex]

c) [latex](A\cup C')\cap(B\cup C')=\{0, 1, 2, 3, 4, 5, 6, 7, 8, 10, 11\}\cap\{0, 1, 2, 4, 5, 6, 7, 8, 10, 11, 12\}=\{0, 1, 2, 4, 5, 6, 7, 8, 10, 11\}[/latex]

Notice that the answers to Exercise 3 are the same as those in Example 3. This is not a coincidence. The following equivalences hold true for sets:

[latex]A\cap(B\cup C)=(A\cap B)\cap C[/latex] and [latex]A\cup(B\cup C)=(A\cup B)\cup C[/latex] $A \cup (B \cup C) = (A \cup B) \cup C .$ These are the associative property for set intersection and set union.
[latex]A \cap B=B \cap A[/latex] and [latex]A\cup B=B\cup A[/latex] $A \cup B = B \cup A .$ These are the commutative property for set intersection and set union.
[latex]A\cap (B\cup C)=(A\cap B)\cup(A\cap C)[/latex] and [latex]A\cup (B\cap C)=(A\cup B)\cap(A\cup C)[/latex] $A \cup (B \cap C) = (A \cup B) \cap (A \cup C) .$ These are the distributive property for sets over union and intersection, respectively.

Proving Equality of Sets Using Venn Diagrams

To prove set equality using Venn diagrams, the strategy is to draw a Venn diagram to represent each side of the equality, then look at the resulting diagrams to see if the regions under consideration are identical.

Augustus De Morgan was an English mathematician known for his contributions to set theory and logic. De Morgan’s law for set complement over union states that [latex](A \cup B)'=A' \cap B'[/latex]. In the next example, we will use Venn diagrams to prove De Morgan’s law for set complement over union is true. But before we begin, let us confirm De Morgan’s law works for a specific example. While showing something is true for one specific example is not a proof, it will provide us with some reason to believe that it may be true for all cases.

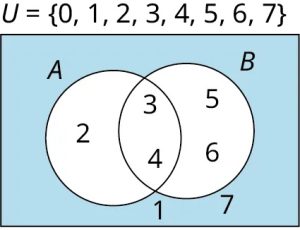
Let [latex]U=\{1, 2, 3, 4, 5, 6, 7\}, A=\{2, 3, 4\}[/latex] $A = {2, 3, 4},$ and [latex]B=\{3, 4, 5, 6\}[/latex] $B = {3, 4, 5, 6} .$ We will use these sets in the equation [latex](A \cup B)'=A' \cap B'[/latex] $(A \cup B)^{'} = A^{'} \cap B^{'} .$

To begin, find the value of the set defined by each side of the equation.

Step 1: [latex]A\cup B[/latex] is the collection of all unique elements in set [latex]A[/latex] or set [latex]B[/latex] or both. [latex]A\cup B=\{2, 3, 4, 5, 6\}[/latex] $A \cup B = {2, 3, 4, 5, 6} .$ The complement of [latex]A[/latex] union [latex]B[/latex], [latex](A\cup B)'[/latex], is the set of all elements in the universal set that are not in [latex]A \cup B[/latex]. So, the left side the equation [latex](A \cup B)'[/latex] is equal to the set [latex]\{1, 7\}[/latex] ${1, 7} .$

Step 2: The right side of the equation is [latex]A' \cap B'[/latex]. [latex]A'[/latex] is the set of all members of the universal set [latex]U[/latex] that are not in set [latex]A[/latex].

[latex]A'=\{1, 5, 6, 7\}[/latex]. Similarly, [latex]B'=\{1, 2, 7\}[/latex]

Step 3: Finally, [latex]A'\cap B'[/latex] is the set of all elements that are in both [latex]A'[/latex] and [latex]B'[/latex] $B^{'} .$ The numbers [latex]1[/latex] and [latex]7[/latex] are common to both sets, therefore, [latex]A' \cap B'=\{1, 7\}[/latex] $A^{'} \cap B^{'} = {1, 7} .$ Because, [latex]\{1, 7\}=\{1, 7\}[/latex] we have demonstrated that De Morgan’s law for set complement over union works for this particular example.

The Venn diagram below depicts this relationship.

A two-set Venn diagram of A and B is given. Set A shows 2, l while set B shows 5, 6. The intersection of the sets shows 3, 4. Outside sets A and B, 1, and 7 are shown. The union of the sets A and B shows (0, 1, 2, 3, 4, 5, 6, 7). — Figure 10. Two set Venn diagram with sets A and B

Example 4

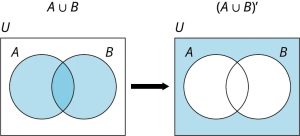
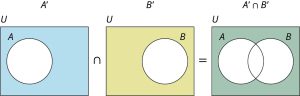
De Morgan’s Law for the complement of the union of two sets [latex]A[/latex] and [latex]B[/latex] states that:

[latex](A \cup B)' = A' \cap B'[/latex] $(A \cup B)^{'} = A^{'} \cap B^{'} .$ Use a Venn diagram to prove that De Morgan’s Law is true.

Step 1: First, draw a Venn diagram representing the left side of the equality. The regions of interest are shaded to highlight the sets of interest. [latex]A \cup B[/latex] is shaded on the left, and [latex](a\cup B)'[/latex] is shaded on the right.

A Venn diagram of the union of two sets and the complement is depicted. A union of the two sets A and B shows the intersection of A and B is shaded while the rest of U is unshaded. The complement of the union of sets A and B shows the area of U shaded while the intersection of A and B is unshaded. — Figure 11. Left Side of De Morgan’s Law

Step 2: Next, draw a Venn diagram to represent the right side of the equation. [latex]A'[/latex] is shaded and [latex]B'[/latex] is shaded. Because [latex]A'[/latex] and

B^{'}

mix to form [latex]A' \cap B'[/latex] is also shaded.

A Venn diagram of the intersection of the complement of two sets is depicted. Complement of A shows A is unshaded while U is shaded. The complement of B shows B is unshaded while U is shaded. A complement of the union of A and B show A intersecting with B. Sets A and B are not shaded while U is shaded. — Figure 12. Right side of the equation for De Morgan’s Law

Step 3: Verify the conclusion. Because the shaded region in the Venn diagram for [latex](A\cup B)'[/latex] matches the shaded region in the Venn diagram for [latex]A' \cap B'[/latex], the two sides of the equation are equal, and the statement is true.

This completes the proof that De Morgan’s law is valid.

Exercise 4

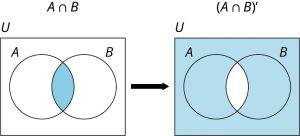
De Morgan’s Law for the complement of the intersection of two sets [latex]A[/latex] and [latex]B[/latex] states that [latex](A \cup B)' = A' \cap B'[/latex] $(A \cup B)^{'} = A^{'} \cap B^{'} .$ Use a Venn diagram to prove that De Morgan’s Law is true.

Solution

The left side of the equation is:

Two Venn diagrams. The first diagram represents A intersection B. It shows two intersecting circles A and B placed inside a rectangle. The rectangle represents U. The intersecting region of the two circles is shaded in blue. The second diagram represents the complement of A intersection B. It shows two intersecting circles A and B placed inside a rectangle. The rectangle represents U. Except for the intersecting region, the other regions of the two circles are shaded in blue. — Figure 13. Venn diagram of intersection of two sets and its complement

The right side of the equation is given by:

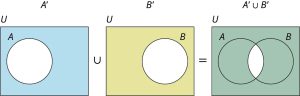
Three Venn diagrams. The first diagram represents A complement. A rectangle U with a circle A on its left. The region inside the rectangle, outside the circle, is shaded in blue. The second diagram represents a B complement. A rectangle U with a circle B on its right. The region inside the rectangle, outside the circle, is shaded in yellow. The third diagram represents A complement union B complement. Two intersecting circles A and B are placed inside a rectangle. The rectangle represents U. Except for the region of intersection, all other regions of the two circles are shaded in green. — Figure 14. Venn diagram of the union of the complement of two sets

Media Attributions

Attendees at a conference with sets: Soup, Sandwich, Salad – Complete Venn diagram Solution © OpenStax is licensed under a CC BY (Attribution) license

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Venn Diagrams with Three Sets

Use the Venn diagram below, which shows the blood types of [latex]100[/latex] people who donated blood at a local clinic, to answer the following questions.

Applying Set Operations to Three Sets

Perform the set operations as indicated on the following sets.

Proving Equality of Sets Using Venn Diagrams

De Morgan’s Law for the complement of the union of two sets [latex]A[/latex] and [latex]B[/latex] states that:

Step 1: First, draw a Venn diagram representing the left side of the equality. The regions of interest are shaded to highlight the sets of interest. [latex]A \cup B[/latex] is shaded on the left, and [latex](a\cup B)'[/latex] is shaded on the right.

Media Attributions

License

Share This Book