Chapter 8 Statistics
8.6 The Normal Distribution
Learning Objectives
By the end of this section, you will be able to:
- Describe the characteristics of the normal distribution
- Apply the 68-95-99.7 percent groups to normal distribution datasets
- Use the normal distribution to calculate a [latex]z[/latex]-score
- Find and interpret percentiles and quartiles
Many datasets that result from natural phenomena tend to have histograms that are symmetric and bell-shaped. Imagine finding yourself with a whole lot of time on your hands and nothing to keep you entertained but a coin, a pencil, and paper. You decide to flip that coin 100 times and record the number of heads. With nothing else to do, you repeat the experiment 10 times total. Using a computer to simulate this series of experiments, here’s a sample for the number of heads in each trial:
54, 51, 40, 42, 53, 50, 52, 52, 47, 54
It makes sense that we’d get somewhere around 50 heads when we flip the coin 100 times, and it makes sense that the result won’t always be exactly 50 heads. In our results, we can see numbers that were generally near 50 and not always 50, like we thought.
Moving toward Normality
Let’s take a look at a histogram for the dataset in our section opener:
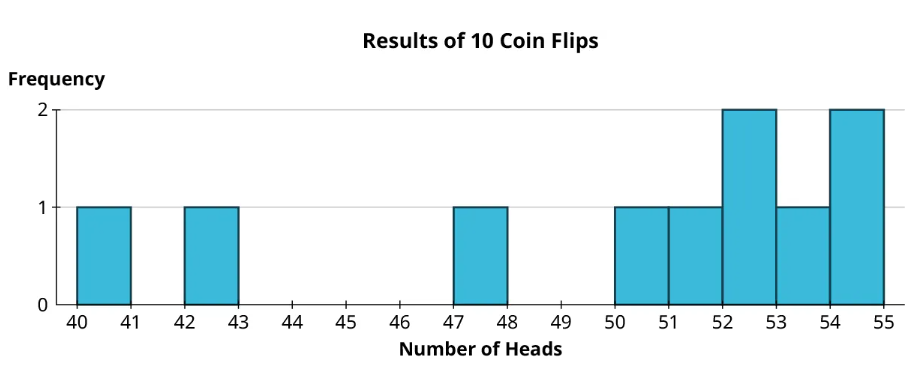
This is interesting, but the data seem pretty sparse. There were no trials where you saw between 43 and 47 heads, for example. Those results don’t seem impossible; we just didn’t flip enough times to give them a chance to pop up. So let’s do it again, but this time we’ll perform 100 coin flips 100 times. Rather than review all 100 results, which could be overwhelming, let’s instead visualize the resulting histogram.
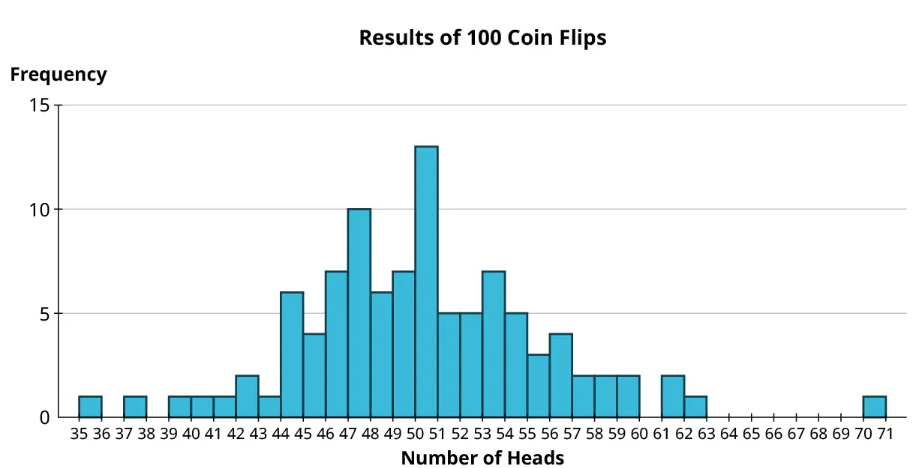
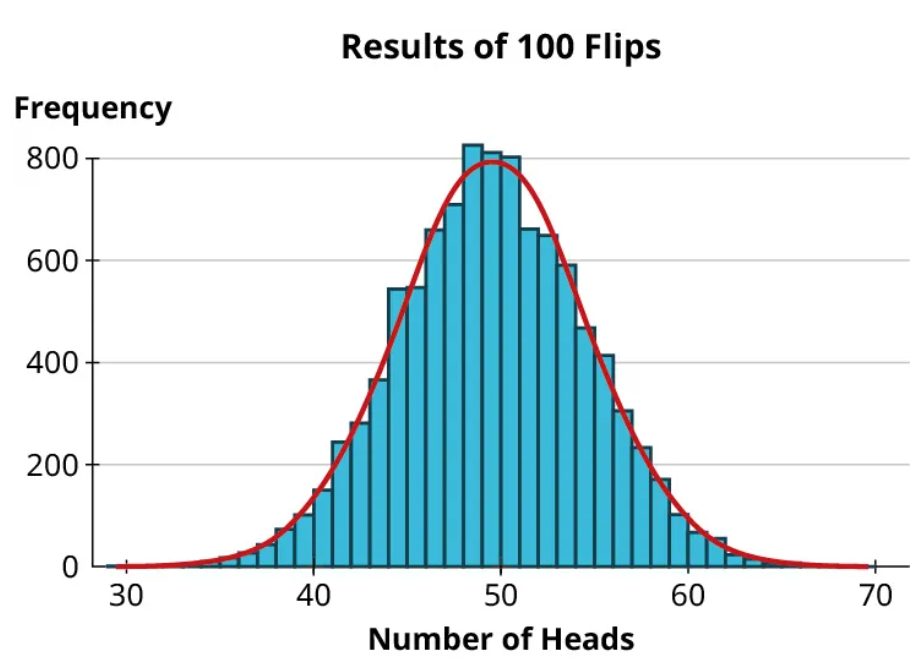
From the histogram, we see that most of the trials resulted in between, say, 44 and 56 heads. There were some more unusual results: one trial resulted in 70 heads, which seems really unlikely (though still possible!). But we’re starting to maybe get a sense of the distribution. More data would help, though. Let’s simulate another 900 trials and add them to the histogram!
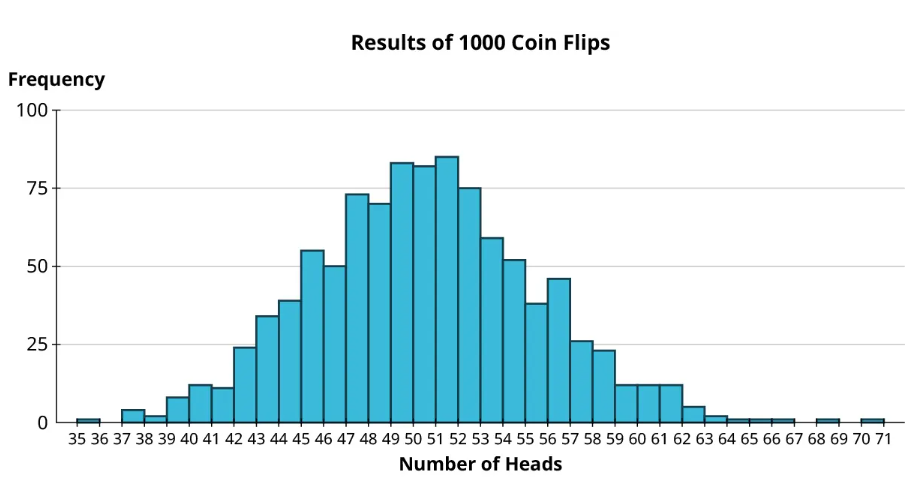
We can still see that 70 is a really unusual observation, though we came close in another trial (one that had 68 heads). Now the distribution is coming more into focus: it looks quite symmetric and bell-shaped. Let’s just go ahead and take this thought experiment to an extreme conclusion: 10,000 trials.
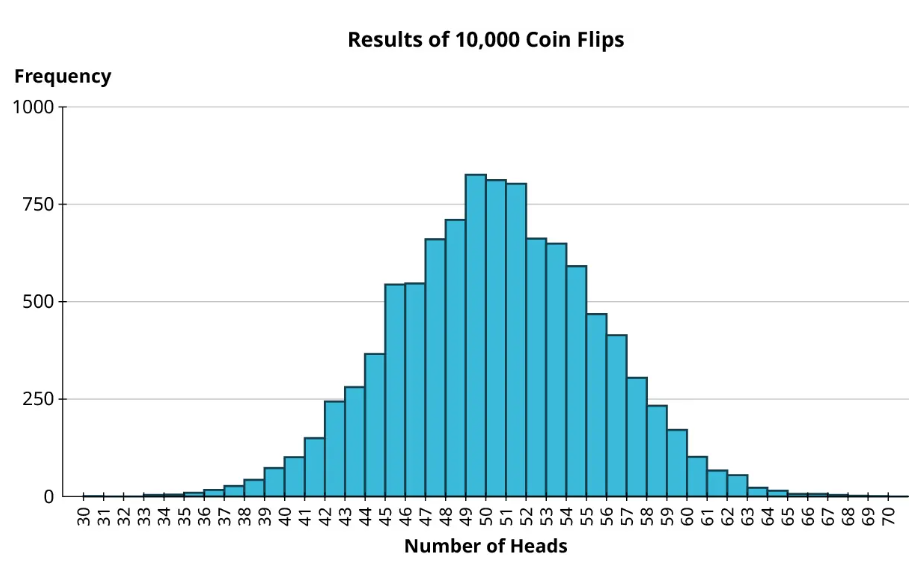
The distribution is pretty clear now. Distributions that are symmetric and bell-shaped like this pop up in all sorts of natural phenomena, such as the heights of people in a population, the circumferences of eggs of a particular bird species, and the numbers of leaves on mature trees of a particular species. All of these have bell-shaped distributions. Additionally, the results of many types of repeated experiments generally follow this same pattern, as we saw with the coin-flipping example; this fact is the basis for much of the work done by statisticians. It’s a fact that’s important enough to have its own name: the Central Limit Theorem.
The Normal Distribution
In the coin flipping example above, the distribution of the number of heads for 10,000 trials was close to perfectly symmetric and bell-shaped:
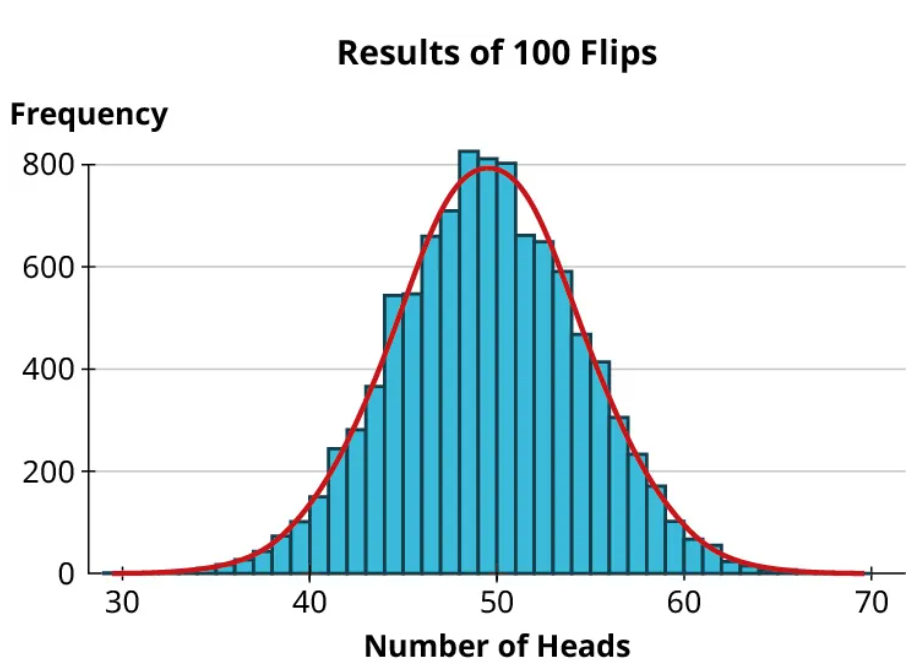
Because distributions with this shape appear so often, we have a special name for them: normal distributions. Normal distributions can be completely described using two numbers we’ve seen before: the mean of the data and the standard deviation of the data. You may remember that we described the mean as a measure of centrality; for a normal distribution, the mean tells us exactly where the center of the distribution falls. The peak of the distribution happens at the mean (and, because the distribution is symmetric, it’s also the median). The standard deviation is a measure of dispersion; for a normal distribution, it tells us how spread out the histogram looks. To illustrate these points, let’s look at some examples.
Example 1
This graph shows three normal distributions. What are their means?

Step 1: Take a look at the three curves on the graph. Since the mean of a normal distribution occurs at the peak, we should look for the highest point on each distribution. Let’s draw a line from each curve’s peak down to the axis so we can see where these peaks occur:

Step 2: The peak of the red (leftmost) distribution occurs over the number 1 on the horizontal axis. Thus, the mean of the red distribution is 1. Similarly, the mean of the blue (middle) distribution is 2, and the mean of the yellow (rightmost) distribution is 3.
Exercise 1
Identify the means of these three distributions:
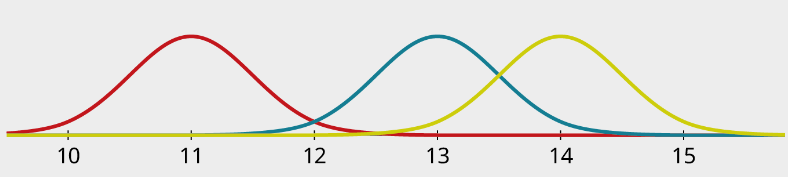
Solution
The red (leftmost) distribution has mean 11, the blue (middle) has mean 13, and the yellow (rightmost) has mean 14.
Example 2
This graph shows three distributions, all with mean 2. What are their standard deviations?
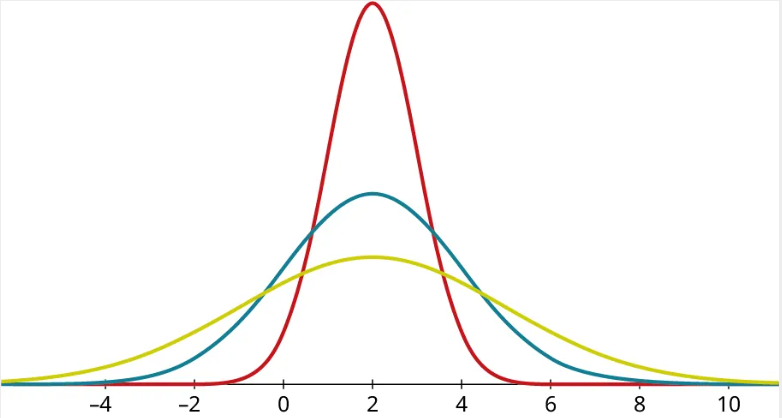
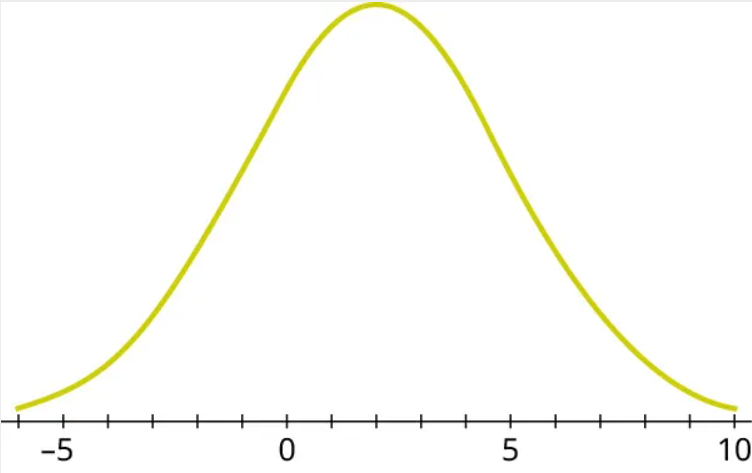
Step 1: Identifying the standard deviation from a graph can be a little bit tricky. Let’s focus in on the yellow (lowest peaked) curve:
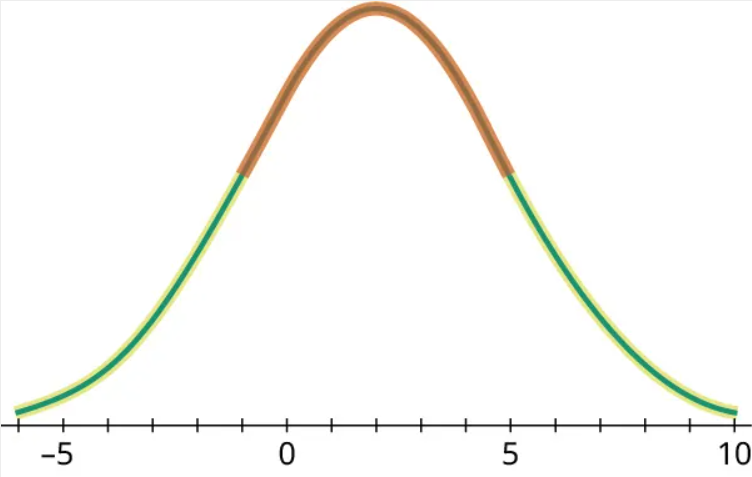
Step 2: Notice that the graph curves downward in the middle and curves upwards on the ends. Highlighted in red is the part that curves downward, and in green, the part that curves upward:
Step 3: The places where the graph changes from curving up to curving down (or vice versa) are called inflection points. Let’s identify where those occur by dropping a line straight down from each:
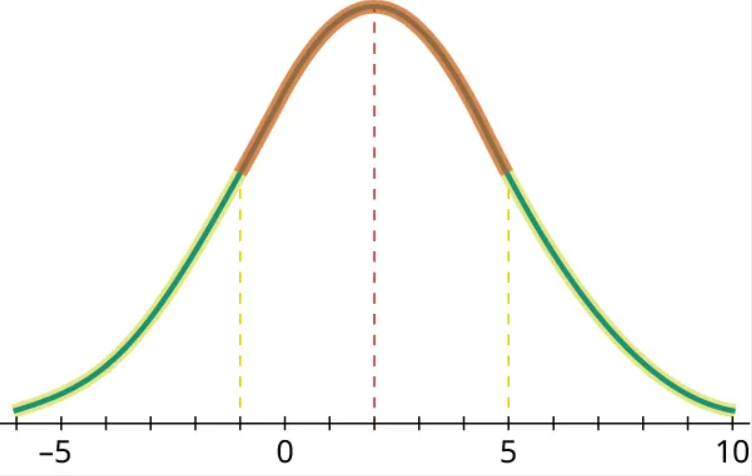
Step 4: We can estimate that the inflection points occur at [latex]x=-1[/latex] and [latex]x=5[/latex]; the mean is at [latex]x=2[/latex] (as shown by the middle dotted line). The difference between the mean and the location of either inflection point is the standard deviation; since [latex]5-2=2-(-1)=3[/latex], we conclude that the standard deviation of the green distribution is 3.
Step 5: Now looking at the other two graphs, let’s first identify the inflection points:
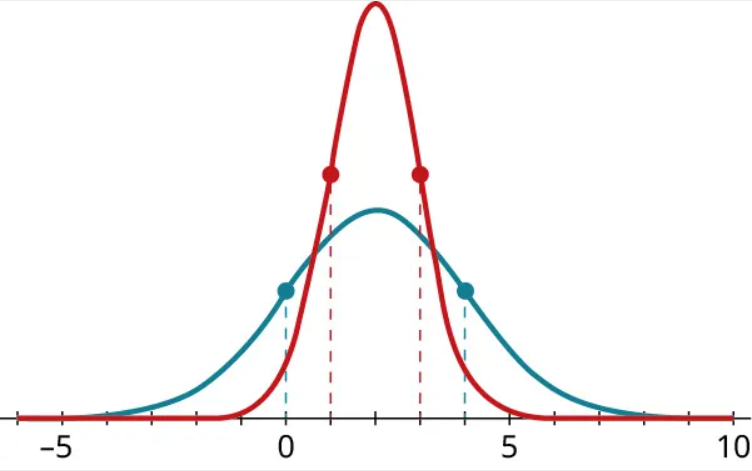
Step 6: The red (tallest peaked) distribution has inflection points at 1 and 3, and the mean is 2. Thus, the standard deviation of the red distribution is [latex]3-2=2-1=1[/latex]. The blue (lower peaked) distribution has inflection points at 0 and 4, and its mean is also 2. So the standard deviation of the blue distribution is 2.
Exercise 2
Estimate the standard deviations of the normal distribution, centered at 5:
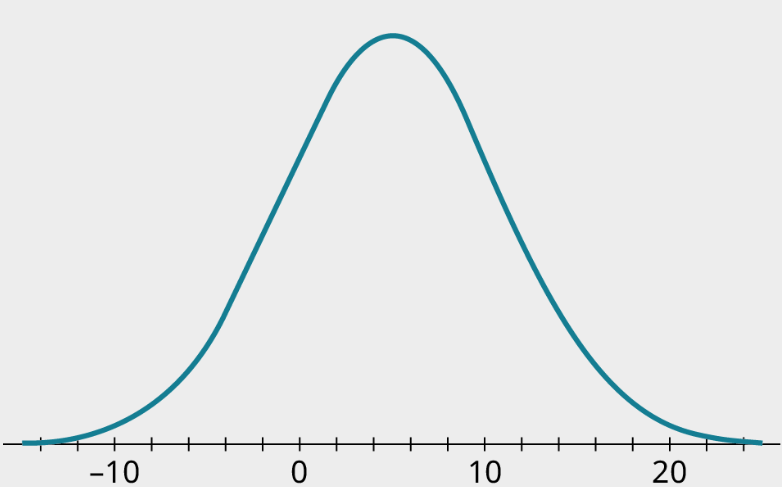
Solution
6
Let’s put it all together to identify a completely unknown normal distribution.
Example 3
Using the graph, identify the mean and standard deviation of the normal distribution.
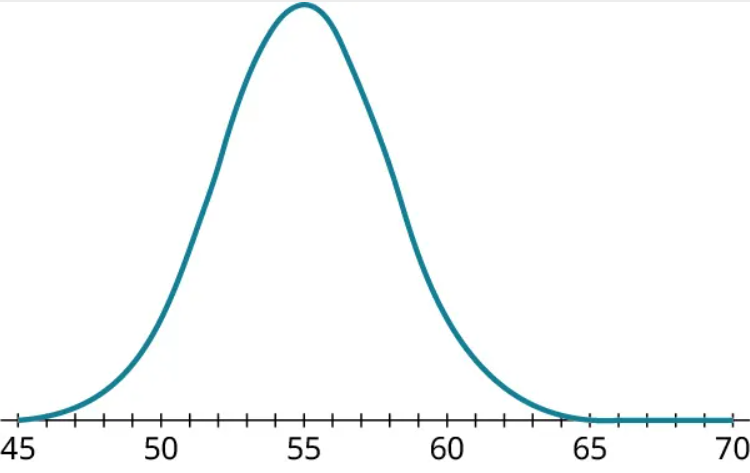
Step 1: Let’s start by putting dots on the graph at the peak and at the inflection points, then drop lines from those points straight down to the axis:
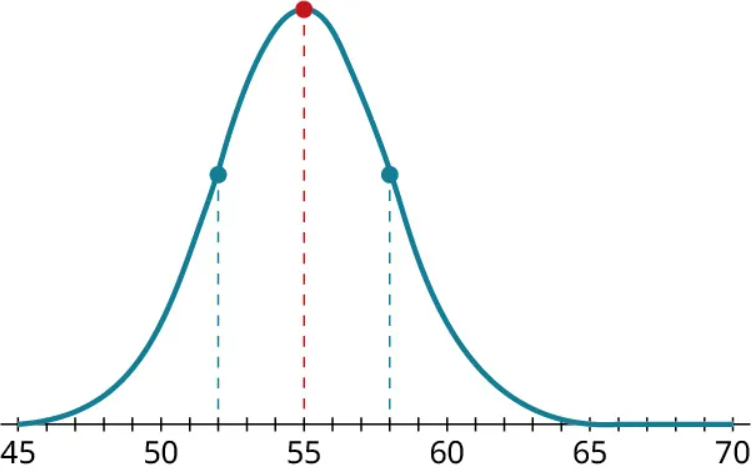
Step 2: From the red (middle) line, we can see that the mean of this distribution is 55. The blue (outermost) lines are each 3 units away from the mean (at 52 and 58), so the standard deviation is 3.
Exercise 3
Identify the mean and standard deviation of this distribution. Anything within 5 on the standard deviation is acceptable.
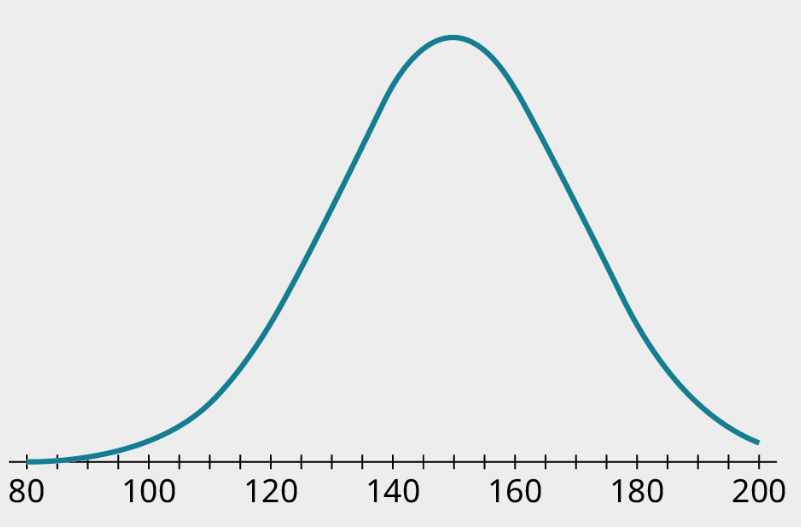
Solution
Mean: 150; standard deviation: 20
Properties of Normal Distributions: The 68-95-99.7 Rule
The most important property of normal distributions is tied to its standard deviation. If a dataset is perfectly normally distributed, then 68% of the data values will fall within one standard deviation of the mean. For example, suppose we have a set of data that follows the normal distribution with mean 400 and standard deviation 100. This means 68% of the data would fall between the values of 300 (one standard deviation below the mean: [latex]400−100=300[/latex]) and 500 (one standard deviation above the mean: [latex]400+100=500[/latex]). Looking at the histogram below, the shaded area represents 68% of the total area under the graph and above the axis:
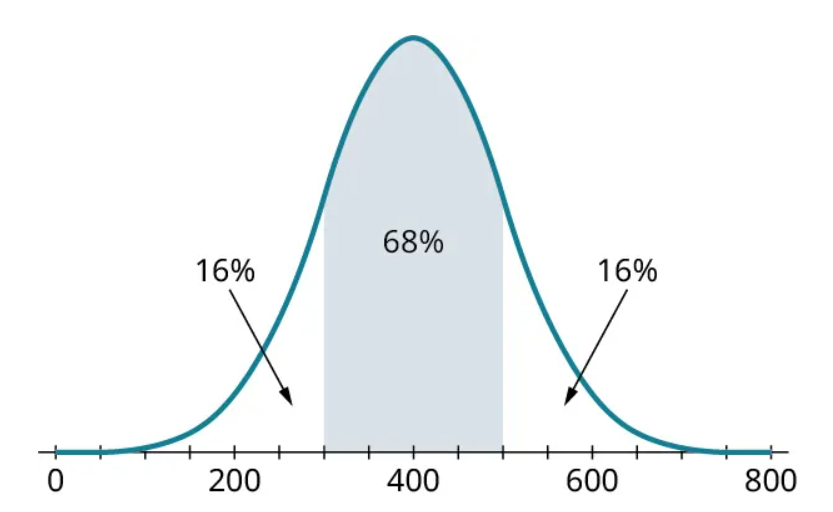
Since 68% of the area is in the shaded region, this means that [latex]100 \%−68 \%=32 \%[/latex] of the area is found in the unshaded regions. We know that the distribution is symmetric, so that 32% must be divided evenly into the two unshaded tails: 16% in each.
Of course, datasets in the real world are never perfect; when dealing with actual data that seem to follow a symmetric, bell-shaped distribution, we’ll give ourselves a little bit of wiggle room and say that approximately 68% of the data fall within 1 standard deviation of the mean.
The rule for 1 standard deviation can be extended to 2 standard deviations. Approximately 95% of a normally distributed dataset will fall within 2 standard deviations of the mean. If the mean is 400 and the standard deviation is 100, that means 95% of the data falls within two standard deviations. We compute the two standard deviations by adding and subtracting 100 to the mean twice. This means 2 standard deviations below the mean is [latex]400–2 \times 100=200[/latex], and two standard deviations above the mean is [latex]400+2 \times 100=600[/latex]. We can visualize this in the following histogram:
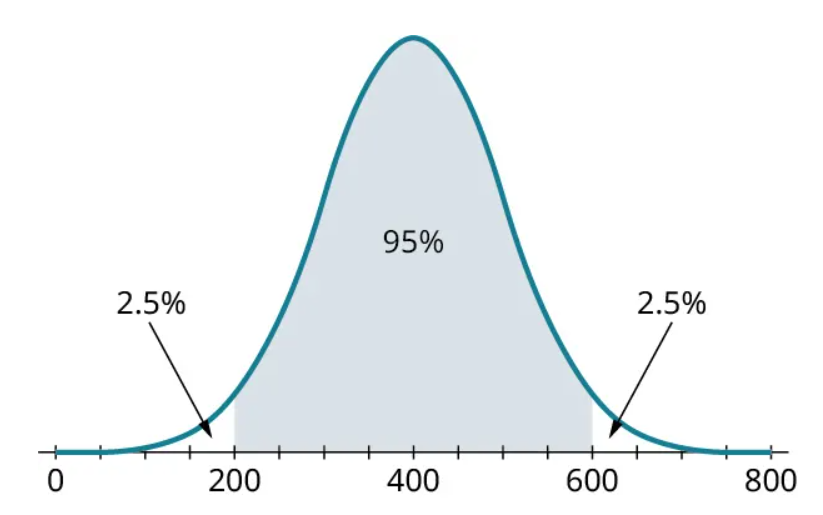
As before, since 95% of the data are in the shaded area, that leaves 5% of the data to go into the unshaded tails. Since the histogram is symmetric, half of the 5% (that’s 2.5%) is in each.
We can even take this one step further: 99.7% of normally distributed data fall within 3 standard deviations of the mean. In this example, we’d see 99.7% of the data between 100 (calculated as [latex]400–3 \times 100=100[/latex]) and 700 (calculated as [latex]400+3 \times 100=700[/latex]). We can see this in the histogram below, although you may need to squint to find the unshaded bits in the tails!
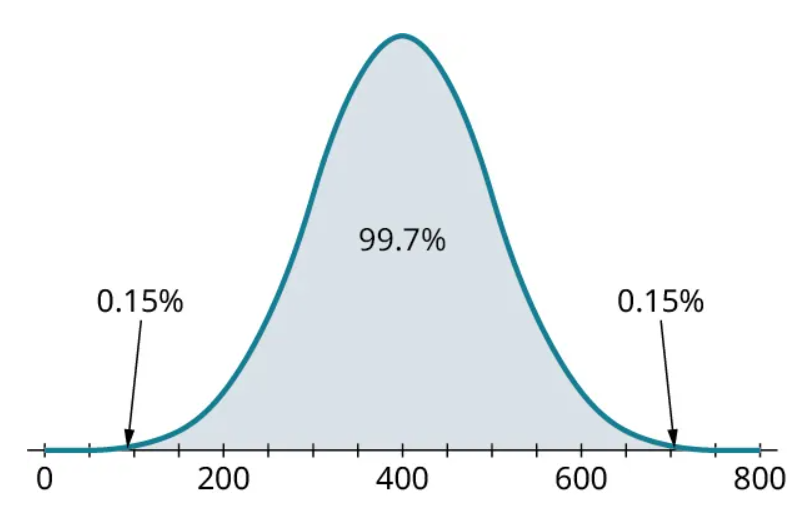
This observation is formally known as the 68-95-99.7 Rule. The following example uses the 68-95-99.7 Rule to find percentages.
Example 4
a) If data are normally distributed with mean 8 and standard deviation 2, what percent of the data falls between 4 and 12?
Let’s look at a table that sets out the data values that are even multiples of the standard deviation (SD) above and below the mean:
| [latex]\text{mean}-3 \times \text{SD}[/latex] | [latex]\text{mean}-2 \times \text{SD}[/latex] | [latex]\text{mean}-2 \times \text{SD}[/latex] | [latex]\text{Mean}[/latex] | [latex]\text{mean}+1 \times \text{SD}[/latex] | [latex]\text{mean}+2 \times \text{SD}[/latex] | [latex]\text{mean}+3 \times \text{SD}[/latex] |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 |
Since 4 and 12 represent 2 standard deviations above and below the mean, we conclude that 95% of the data will fall between them.
b) If data are normally distributed with mean 25 and standard deviation 5, what percent of the data falls between 20 and 30?
| [latex]\text{mean}-3 \times \text{SD}[/latex] | [latex]\text{mean}-2 \times \text{SD}[/latex] | [latex]\text{mean}-2 \times \text{SD}[/latex] | [latex]\text{Mean}[/latex] | [latex]\text{mean}+1 \times \text{SD}[/latex] | [latex]\text{mean}+2 \times \text{SD}[/latex] | [latex]\text{mean}+3 \times \text{SD}[/latex] |
| 10 | 15 | 20 | 25 | 30 | 35 | 40 |
We can see that 20 and 30 represent 1 standard deviation above and below the mean, so 68% of the data fall in that range.
(c) If data are normally distributed with mean 200 and standard deviation 15, what percent of the data falls between 155 and 245?
| [latex]\text{mean}-3 \times \text{SD}[/latex] | [latex]\text{mean}-2 \times \text{SD}[/latex] | [latex]\text{mean}-2 \times \text{SD}[/latex] | [latex]\text{Mean}[/latex] | [latex]\text{mean}+1 \times \text{SD}[/latex] | [latex]\text{mean}+2 \times \text{SD}[/latex] | [latex]\text{mean}+3 \times \text{SD}[/latex] |
| 155 | 170 | 185 | 200 | 215 | 230 | 245 |
Since 155 and 245 are 3 standard deviations above and below the mean, we know that 99.7% of the data will fall between them.
Exercise 4
Example 5
a) If data are distributed normally with mean 100 and standard deviation 20, between what two values will 68% of the data fall?
The 68-95-99.7 Rule tells us that 68% of the data will fall within 1 standard deviation of the mean. So to find the values we seek, we’ll add and subtract 1 standard deviation from the mean: [latex]100−1 \times 20=80[/latex] and [latex]100+1 \times 20=120[/latex]. Thus, we know that 68% of the data fall between 80 and 120.
b) If data are distributed normally with mean 0 and standard deviation 15, between what two values will 95% of the data fall?
Using the 68-95-99.7 Rule again, we know that 95% of the data will fall within 2 standard deviations of the mean. Let’s add and subtract 2 standard deviations from that mean: [latex]0−2 \times 15=−30[/latex] and [latex]0+2 \times 15=30[/latex]. So 95% of the data will fall between -30 and 30.
c) If data are distributed normally with mean 14 and standard deviation 2, between what two values will 99.7% of the data fall?
Once again, the 68-95-99.7 Rule tells us that 99.7% of the data will fall within 3 standard deviations of the mean. So let’s add and subtract 3 standard deviations from the mean: [latex]14-3 \times 2=8[/latex] and [latex]14+3 \times 2=20[/latex]. Thus, we conclude that 99.7% of the data will fall between 8 and 20.
Exercise 5
a) If data are distributed normally with mean 70 and standard deviation 5, between what two values will 68% of the data fall?
b) If data are distributed normally with mean 40 and standard deviation 7, between what two values will 95% of the data fall?
c) If data are distributed normally with mean 200 and standard deviation 30, between what two values will 99.7% of the data fall?
Solution
a) 65 and 75
b) 26 and 54
c) 110 and 290
There are more problems we can solve using the 68-95-99.7 Rule, but first we must understand what the rule implies. Remember, the rule says that 68% of the data falls within 1 standard deviation of the mean. Thus, with normally distributed data with mean 100 and standard deviation 10, we have this distribution:
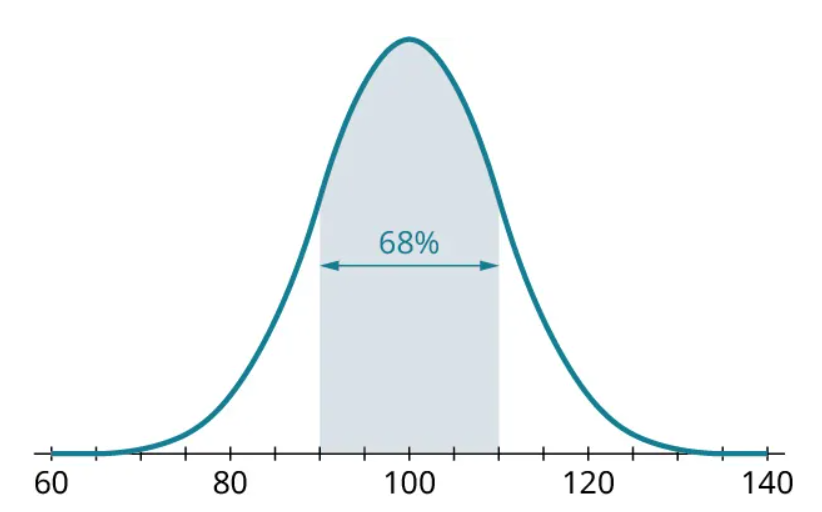
Since we know that 68% of the data lie within 1 standard deviation of the mean, the implication is that 32% of the data must fall beyond 1 standard deviation away from the mean. Since the histogram is symmetric, we can conclude that half of the 32% (or 16%) is more than 1 standard deviation above the mean, and the other half is more than 1 standard deviation below the mean:
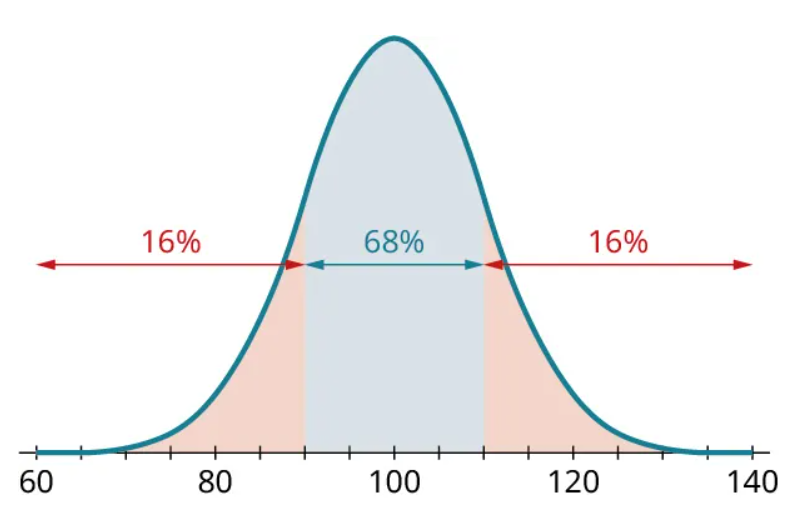
Further, we know that the middle 68% can be split in half at the peak of the histogram, leaving 34% on either side:
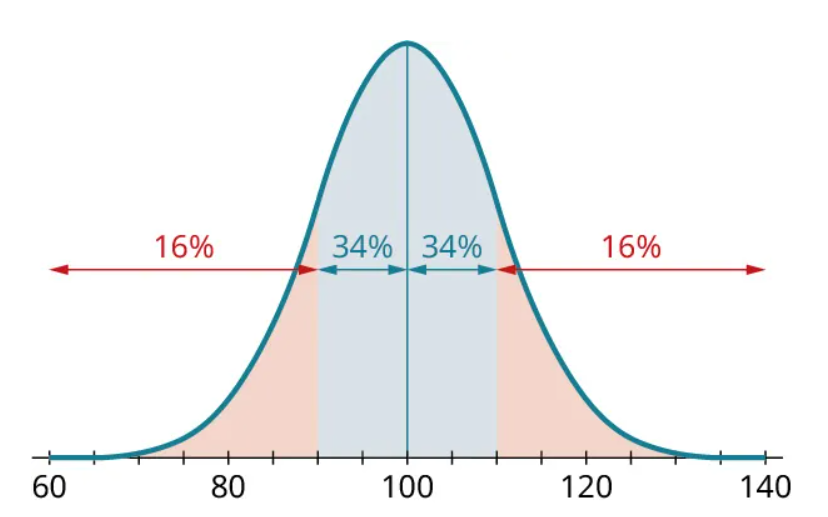
So just the “68” part of the 68-95-99.7 Rule gives us four other proportions in addition to the 68% in the rule. Similarly, the “95” and “99.7” parts each give us four more proportions:
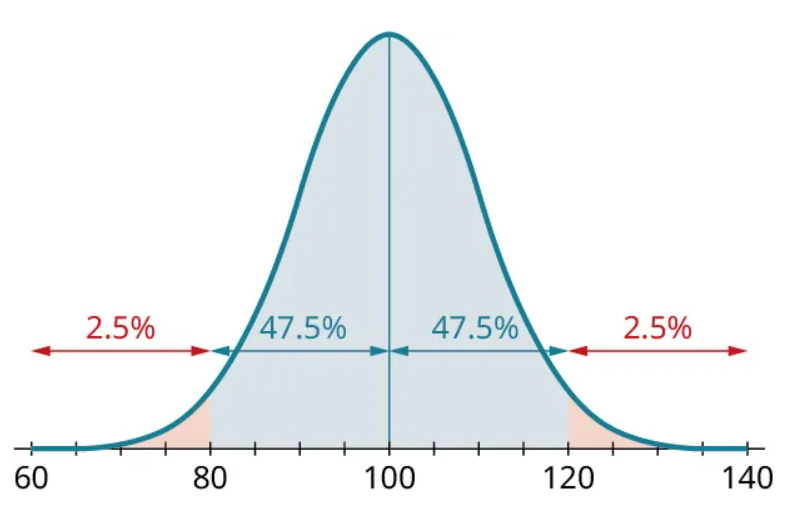
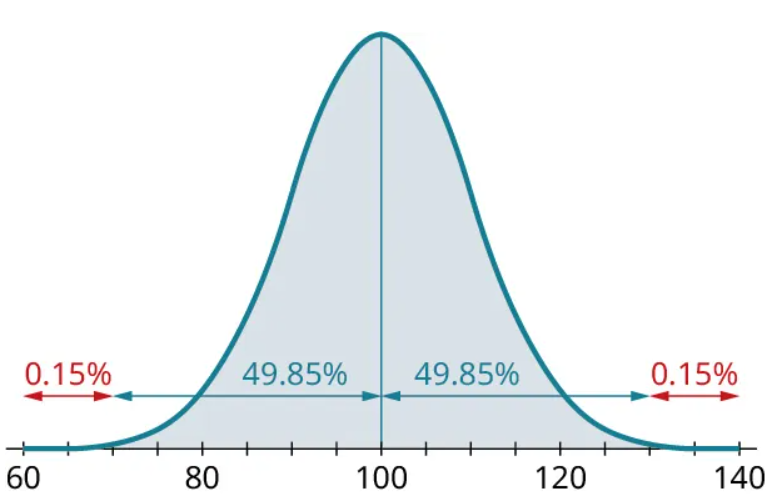
We can put all these together to find even more complicated proportions. For example, since the proportion between 100 and 120 is 47.5% and the proportion between 100 and 110 is 34%, we can subtract to find that the proportion between 110 and 120 is [latex]47.5−34=13.5 \%[/latex]:
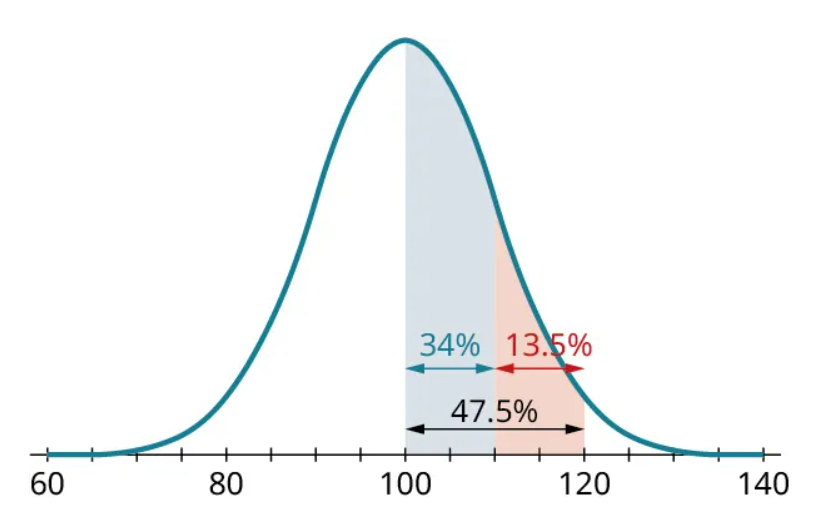
Example 6
Assume that we have data that are normally distributed with mean 80 and standard deviation 3.
a) What proportion of the data will be greater than 86?
Before we can answer any questions, we must mark off sections that are multiples of the standard deviation away from the mean:
Figure 28. Normal distributionTo figure out what proportion of the data will be greater than 86, let’s start by shading in the area of data that are above 86 in our figure, or the data more than 2 standard deviations above the mean.
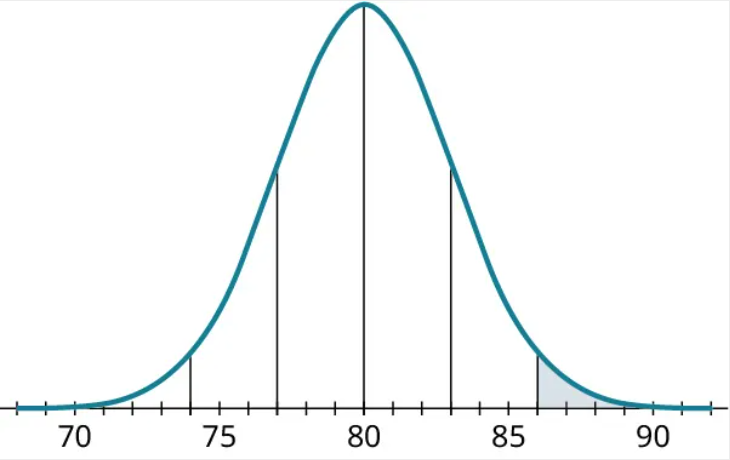
This proportion is 2.5%.
b) What proportion of the data will be between 74 and 77?
To figure out what proportion of the data will be between 74 and 77, let’s start by shading in that area of data. These are data that are more than 1 but less than 2 standard deviations below the mean.
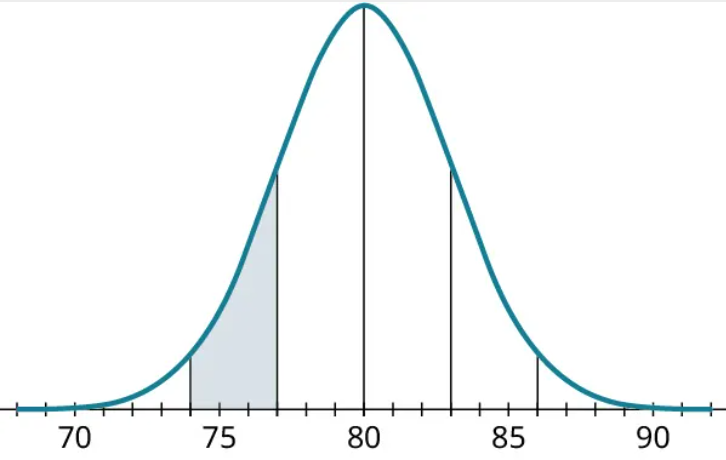
We know that the proportion of data less than 2 standard deviations below the mean is 47.5%, and we know that 34% of the data is less than 1 standard deviation below the mean:
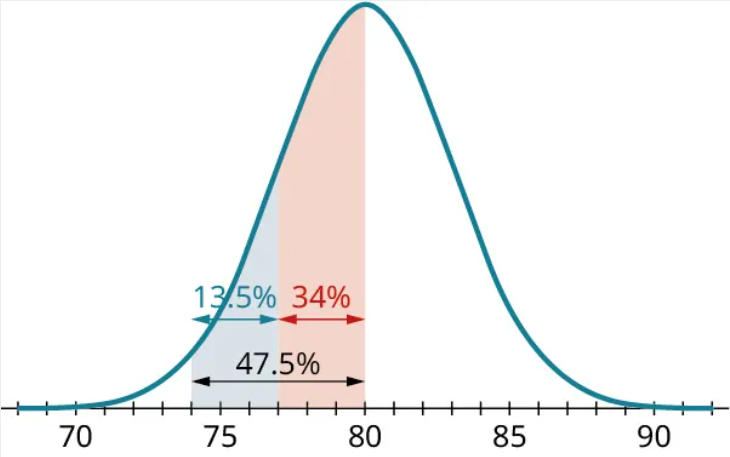
Subtracting, we see that the proportion of data between 74 and 77 is 13.5%.
c) What proportion of the data will be between 74 and 83?
To figure out what proportion of the data will be between 74 and 83, let’s start by shading in that area of data in our figure.
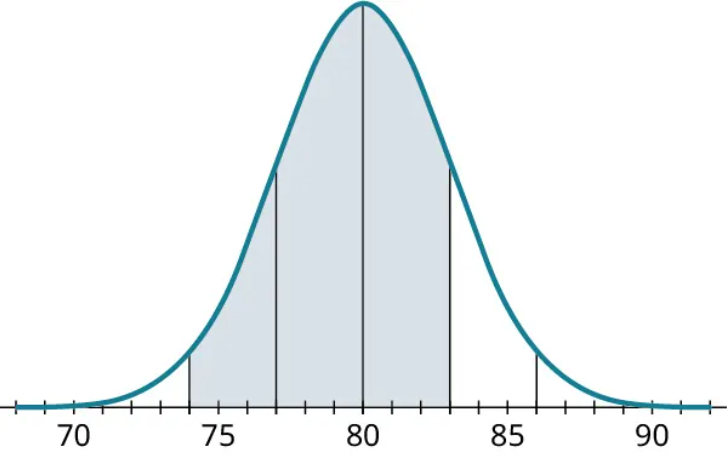
Next, we’ll break this region into two pieces at the mean:
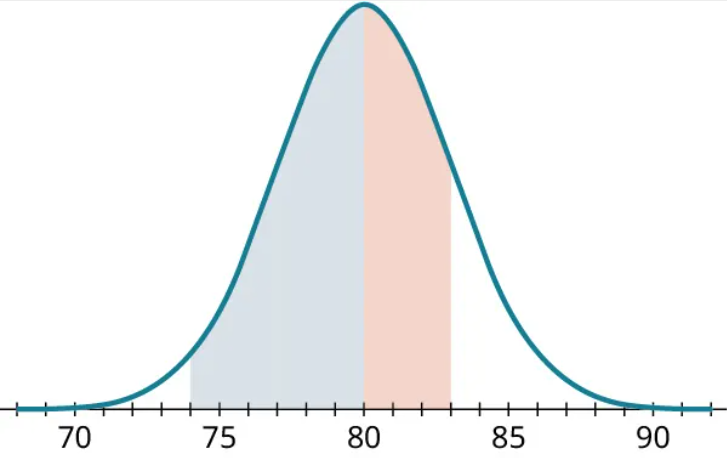
We know the blue (leftmost) region represents 47.5% of the data. The red (rightmost) region covers 34% of the data. Adding those together, the proportion we want is 81.5%.
Exercise 6
Suppose we have data that are normally distributed with mean 500 and standard deviation 100. What proportions of the data fall in these ranges?
a) 300 to 500
b) 600 to 800
c) 400 to 700
Solution
a) 47.5%
b) 15.85%
c) 81.5%
Standardized Scores
When we want to apply the 68-95-99.7 Rule, we must first figure out how many standard deviations above or below the mean our data fall. This calculation is common enough that it has its own name: the standardized score. Values above the mean have positive standardized scores, while those below the mean have negative standardized scores. Since it’s common to use the letter [latex]z[/latex] to represent a standard score, this value is also often referred to as a [latex]z[/latex]-score.
So far, we’ve only really considered [latex]z[/latex]-scores that are whole numbers, but in general they can be any number at all. For example, if we have data that are normally distributed with mean 80 and standard deviation 6, the value 85 is five units above the mean, which is less than 1 standard deviation. Dividing by the standard deviation, we get [latex]\frac{5}{6}[/latex]. Since 85 is [latex]\frac{5}{6}[/latex] of 1 standard deviation above the mean, we’d say that the standardized score for 85 is [latex]z=\frac{5}{6}[/latex] (which is positive, since [latex]85>80[/latex]). This calculation describes the way we compute standardized scores.
Formula
If [latex]x[/latex] is a member of a normally distributed dataset with mean [latex]\mu[/latex] and standard deviation [latex]\sigma[/latex], then the standardized score for [latex]x[/latex] is
[latex]z=\frac{x-\mu}{\sigma}[/latex].
If you know a [latex]z[/latex]-score but not the original data value [latex]x[/latex], you can find it by solving the previous equation for [latex]x[/latex]:
[latex]x=\mu + z \times \sigma[/latex].
The symbols [latex]\mu[/latex] and [latex]\sigma[/latex] are the Greek letters mu and sigma. They are the analogues of the English letters [latex]m[/latex] and [latex]s[/latex], which stand for mean and standard deviation.
If you convert every data value in a dataset into its z-score, the resulting set of data will have mean 0 and standard deviation 1. This is why we call these standardized scores: the normal distribution with mean 0 and standard deviation 1 is often called the standard normal distribution.
Example 7
Suppose we have data that are normally distributed with mean 50 and standard deviation 6. Compute the standardized scores (rounded to three decimal places) for these data values:
a) 52
We’ll plug the given values into the formula. Remember, the mean is [latex]\mu=50[/latex] and the standard deviation is [latex]\sigma=6[/latex]:
[latex]z=\frac{x-\mu}{\sigma}=\frac{52-50}{6}=0.333[/latex]
b) 40
We’ll plug the given values into the formula. Remember, the mean is [latex]\mu=50[/latex] and the standard deviation is [latex]\sigma=6[/latex]:
[latex]z=\frac{x-\mu}{\sigma}=\frac{40-50}{6}=-1.667[/latex]
c) 68
We’ll plug the given values into the formula. Remember, the mean is [latex]\mu=50[/latex] and the standard deviation is [latex]\sigma=6[/latex]:
[latex]z=\frac{x-\mu}{\sigma}=\frac{68-50}{6}=3[/latex]
Exercise 7
Suppose we have data that are normally distributed with mean 75 and standard deviation 5. Compute standardized scores for each of these data values:
a) 66
b) 83
c) 72
Solution
a) -1.8
b) 1.6
c) -0.6
Example 8
Suppose we have data that are normally distributed with mean 10 and standard deviation 2. Convert the following standardized scores into data values.
a) 1.4
We’ll use the formula previously introduced to convert [latex]z[/latex]-scores into [latex]x[/latex]-values. In this case, the mean is [latex]\mu=10[/latex] and the standard deviation is [latex]\sigma=2[/latex]:
[latex]x=\mu+z \times \sigma = 10+1.4 \times 2=12.8[/latex]
b) −0.9
We’ll use the formula previously introduced to convert [latex]z[/latex]-scores into [latex]x[/latex]-values. In this case, the mean is [latex]\mu=10[/latex] and the standard deviation is [latex]\sigma=2[/latex]:
[latex]x=\mu+z \times \sigma = 10+ (-0.9) \times 2=8.2[/latex]
c) 3.5
We’ll use the formula previously introduced to convert [latex]z[/latex]-scores into [latex]x[/latex]-values. In this case, the mean is [latex]\mu=10[/latex] and the standard deviation is [latex]\sigma=2[/latex]:
[latex]x=\mu+z \times \sigma = 10+3.5 \times 2=17[/latex]
Exercise 8
Suppose you have a normally distributed dataset with mean 2 and standard deviation 20. Convert these standardized scores to data values:
a) –2.3
b) 1.4
c) 0.2
Solution
a) -44
b) 30
c) 6
Media Attributions
- 8.6 01 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 02 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 03 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 04 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 05 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 06 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 07 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 08 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 09 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 10 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 11 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 12 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 13 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 14 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 15 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 16 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 17 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 18 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 19 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 20 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 21 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 22 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 23 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 24 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 25 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 26 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 27 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 29 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 30 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 31 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 32 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
- 8.6 33 © OpenStax Contemporary Math is licensed under a CC BY (Attribution) license
how many standard deviations above or below the mean our data fall

