We can imagine this situation as three distinct time phases, each with a different interest rate.

To handle the change of interest rates, it is easiest to imagine that each time the interest rate changes, we withdraw all our money and then redeposit it into a new account at a different rate.

For the first year:

[latex]P = $15,000, r = 0.06, t = 1 \text{ year}, k = 12[/latex]

Using the compound interest equation, we find the balance after 1 year would be:

[latex]A = $15,925.17[/latex]

We can then use this as the principal for the next 2 years at a different rate, as if we had withdrawn that money and reinvested it at 4%:

[latex]P = $15,925.17, r = 0.04, t = 2 \text{ years}, k = 12[/latex]

Using the compound interest equation, we find the balance after these next 2 years would be:

[latex]A = $17,249.24[/latex]

Using that as the principal for the last 3 years:

[latex]P = $17,249.24, r = 0.025, t = 3 \text{ years}, k = 12[/latex]

Using the compound interest equation, we find the balance at the end would be:

[latex]A = $18,591.23[/latex]

After the 6 years, the final balance would be $18,591.23.

Jenny plans to retire at age 65 and estimates she will need $48,000 a year in retirement for 30 years. To save for retirement, she plans to put money every month into her 401(k) plan at work. If Jenny is currently 25, how much will she need to save each month to meet her retirement goal, assuming her retirement accounts earn an average of 7% per year?

We can think about this as two separate phases: the accumulation phase and the spending phase. We assume Jenny starts with no money in the beginning and will completely spend down her account by the time she’s 95.

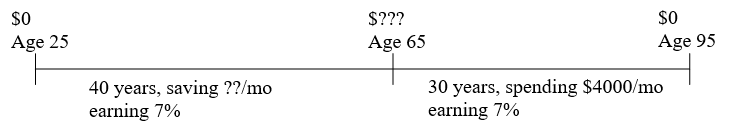
To decide which phase to start with, we look to see which we have the most information for. In the first phase, we don’t know how much she will save each month, and we don’t know the ending balance of the account. For the second phase, we know everything except the starting balance of the account, so we will start the problem in the second phase. Basically, we are going to work the problem backward, using her spending requirement to determine how much she needs at retirement, then use that value to determine how much she needs to save each month.

The second phase is a payout annuity problem, where:

[latex]w = $4,000, r = 0.07, t = 30, k = 12[/latex]

Using the payout annuity formula to find the principal gives:

[latex]P = $601,230.27[/latex]

This is how much Jenny will need at retirement to meet her spending needs and fills in a part of our timeline:

Now we can work on the first phase, which is a savings annuity problem where the desired end balance is the $601,230.27 we just found.

[latex]A = $601,230.27, r = 0.07, t = 40, k = 12[/latex]

Using the savings annuity formula to solve for the deposit amount gives:

[latex]d = 229.06[/latex]

Jenny will need to save $229.06 per month to meet her retirement goals.

To work this problem using the TVM Solver calculator, click here.

The challenge with this problem is that our savings annuity formula assumed that our account balance started at zero. While we could try to build a new formula to handle this situation, we can more easily envision it as two different money streams, as if the original $70,000 is invested in a different account than future contributions.

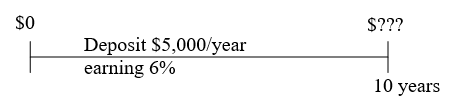
In the first stream of money, we have $70,000 earning 6% interest for 10 years, which is a basic compound interest problem:

[latex]P = $70,000, r = 0.06, t = 10, k = 1[/latex]

Using the compound interest formula to solve for the ending balance:

[latex]A = $125,359.34[/latex]

In the second stream of money, we are depositing $5,000 a year, a savings annuity problem:

[latex]d = $5,000, r = 0.06, t = 10, k = 1[/latex]

Using the savings annuity formula to find the ending balance:

[latex]A = $65,903.97[/latex]

Now that we know the ending balance of each stream of money, we can add those together to find the total balance of the account at the end of the 10 years:

[latex]$125,359.34 + $65,903.97 = $191,263.31[/latex]

To work this problem using the TVM Solver calculator, click here.

To determine the monthly payments for the refinance, we first need to know how much the refinanced loan amount will be. The amount refinanced will be the same as the remaining loan balance on the original loan after 5 years. We will start by finding the details of the original loan.

The 20% down payment will be [latex]$260,000(0.20) = $52,000[/latex], leaving $208,000 to be financed.

We start by finding the payments on the original loan:

[latex]P = $208,000, r = 0.03, t = 30, k = 12[/latex]

Using the loan formula to solve for the payment,

[latex]PMT = $876.94[/latex]

Now we can find the remaining balance on the original loan after 5 years. As discussed in the last section, we can find this by determining the amount of loan that can be paid off with payments of $876.94 in the remaining 25 years:

[latex]PMT = $876.94, r = 0.03, t = 25, k = 12[/latex]

Using the loan formula to solve for the remaining balance,

[latex]P = $184,926.00[/latex]

So after 5 years, the remaining balance on the loan is $184,926.00, and that is the amount we will refinance in a new 30-year mortgage at the fixed 4% rate:

[latex]P = $184,926.00, r = 0.04, t = 30, k = 12[/latex]

Solving for the new payment amount:

[latex]PMT = $882.87[/latex]

Because of the higher interest rate, the monthly payment increased even though the loan amount was less at refinance. Most likely this increase is much smaller than the one the couple would have faced from the original loan’s rate adjusting.

Notice also that because of the refinance, the couple will end up making payments for a total of 35 years on the house.

In those first 5 years, the couple paid a total of [latex]$876.94(12)(5) = $52,616.40[/latex] and reduced the loan balance by [latex]$208,000 - $184,926 = $23,074[/latex], meaning they paid $29,542.40 in interest during the first 5 years.

In the remaining 30 years, the couple will pay [latex]$882.87(12)(30) = $317,833.20[/latex] and reduce the loan balance by $184,926, meaning they will pay $132,907.20 in interest during these 30 years.

In total, the couple will pay [latex]$132,907.20 + $29,542.40 = $162,449.60[/latex] in interest over the 35 years.

To work this problem using the TVM Solver calculator, click here.