Chapter 4 Finance
4.6 TVM Solver Calculator
Learning Objectives
By the end of this section, you will be able to:
- Solve annuities, payout annuities, and loans problems with the TVM Solver application
This section presents an alternate way to solve annuities, payout annuities, and loans problems using a Time Value Money Solver (TVM Solver) application. The examples and exercises in this section are the same examples and exercises from Section 4.2 through 4.5. There are many applications that exist, but one free resource is the Geogebra TVM Solver. You can use the link to open a new webpage with the calculator, or use the one located in the Back Matter of this textbook.
TVM Solver
[latex]N[/latex] is the total number of payments that are made.
[latex]I\%[/latex] is the interest rate, written as a percentage.
[latex]PV[/latex] is the present value. [latex]PV=0[/latex] when you are trying to save money (for example, in savings annuities).
[latex]PMT[/latex] is the payment amount. PMT will always be a negative number when you are typing it into the TVM Solver.
[latex]FV[/latex] is the future value. [latex]FV=0[/latex] when you are paying something off (for example, in payout annuities and loans)
[latex]P/Y[/latex] is the number of payments per year.
[latex]C/Y[/latex] is the number of times the interest is compounded per year.
Note: [latex]P/Y[/latex] and [latex]C/Y[/latex] are always going to be the same number. Some problems may not specify the number of times the interest is compounded per year, and in that case, you will use the same number that you use for [latex]P/Y[/latex].
Finding Interest
In annuities problems, the goal is to save money, meaning [latex]PV[/latex] will be 0 because there is no money in the account when it opens, and [latex]FV[/latex] will always be a value greater than 0. Interest can be found by using the following formula:
- [latex]\text{Interest}=FV-N \times PMT[/latex]
In payout annuities and loans problems, [latex]PV[/latex] is the amount that is in the annuity at the start of the annuity or the loan amount, so [latex]PV[/latex] is going to be a number greater than 0. [latex]FV[/latex] will be 0 because the annuity will have no money in it or the loan will be worth $0 in the future. For these problems, interest can be found by using the following formula:
- [latex]\text{Interest}=N \times PMT-PV[/latex]
Let’s take a look at some examples from Sections 4.2-4.5 and see how we would work the same problems using the TVM Solver. Note that the answers to these problems may be a little different than the problems in Sections 4.2-4.5 due to rounding.
Examples from Section 4.2
A traditional individual retirement account (IRA) is a special type of retirement account in which the money you invest is exempt from income taxes until you withdraw it. If you deposit $100 each month into an IRA earning 6% interest, how much will you have in the account after 20 years?
[latex]N = 20 \times 12 = 240[/latex] because you are making monthly deposits for 20 years.
[latex]I\% = 6[/latex] because the interest rate is 6%.
[latex]PV = 0[/latex] because you are saving money.
[latex]PMT = -100[/latex] because you are depositing $100 into the account.
[latex]FV[/latex] is what you want to know.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
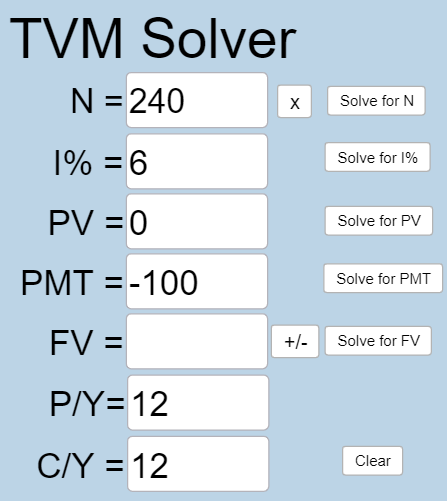
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for FV}\\ \hline \end{array}\;[/latex] button.

The account will grow to $46,204.09 in 20 years.
To find the interest, we can plug values for [latex]FV[/latex], [latex]N[/latex], and [latex]PMT[/latex] into the interest formula:
[latex]\text{Interest}=46204.09 - 240 \times 100=22,204.09[/latex]
So, you made $22,204.09 in interest.
To return to Section 4.2, click here.
You want to have $200,000 in your account when you retire in 30 years. Your retirement account earns 8% interest. How much do you need to deposit each month to meet your retirement goal?
[latex]N = 30 \times 12 = 360[/latex] because you are making monthly deposits for 30 years.
[latex]I\% = 8[/latex] because the interest rate is 8%.
[latex]PV = 0[/latex] because you are saving money.
[latex]PMT[/latex] is what you want to know.
[latex]FV = 200,000[/latex] because you want to have $200,000 in the account in the future.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for PMT}\\ \hline \end{array}\;[/latex]button.
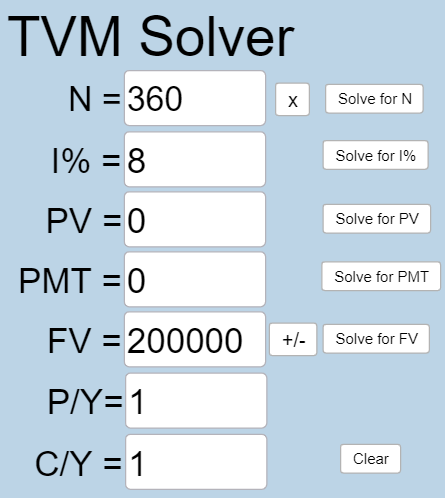
So you would need to deposit $134.09 each month to have $200,000 in 30 years if your account earns 8% interest.

Notice that even though the TVM Solver gave us the answer as a negative number, when we talk about payments, we talk about them as positive numbers. So, [latex]PMT[/latex] will always be negative when we plug [latex]PMT[/latex] into the TVM Solver, but it will be positive in the interest formula and when it is the solution to our problem.
To return to Section 4.2, click here.
If you invest $100 each month into an account earning 3% compounded monthly, how long will it take the account to grow to $10,000?
This is a savings annuity problem since we are making regular deposits into the account.
[latex]N[/latex] is what you want to know.
[latex]I\% = 3[/latex] because the interest rate is 3%.
[latex]PV = 0[/latex] because you are saving money.
[latex]PMT =-100[/latex] because you make payments of $100.
[latex]FV = 10,000[/latex] because you want to have $10,000 in the account in the future.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for N}\\ \hline \end{array}\;[/latex] button.
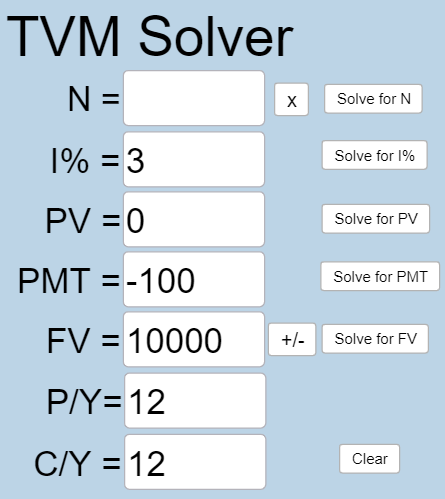
We get that [latex]N = 89.37[/latex] months. Our solution is in months because [latex]N[/latex] tells us how many payments are made in total, and you are making monthly payments. If we wanted our solution in years, we could figure it out with a simple conversion.
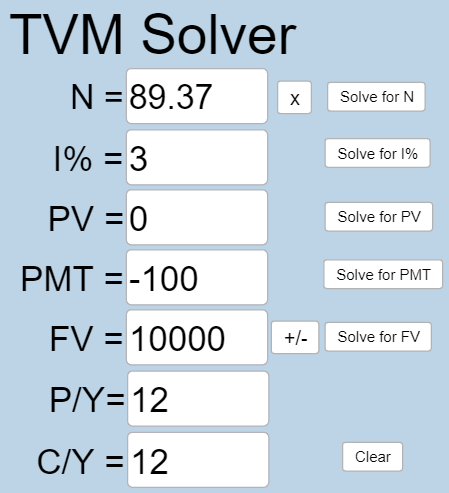
[latex]89.37 \text{ months} \times \frac{1 \text{ year}}{12 \text{ months}}=7.45[/latex] years
To return to Section 4.2, click here.
Examples from Section 4.3
After retiring, you want to be able to take $1000 every month for a total of 20 years from your retirement account. The account earns 6% interest. How much will you need in your account when you retire?
[latex]N = 20 \times 12 = 240[/latex] because you are taking making monthly withdrawals for 20 years.
[latex]I\% = 6[/latex] because the interest rate is 6%.
[latex]PV[/latex] is what you want to want to know.
[latex]PMT =-1000[/latex] because you will make withdrawals of $1000.
[latex]FV = 0[/latex] because after you’ve made all withdrawals, the account has no money in it.
[latex]P/Y=12[/latex] because you are making 12 withdrawals per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for PV}\\ \hline \end{array}\;[/latex] button.
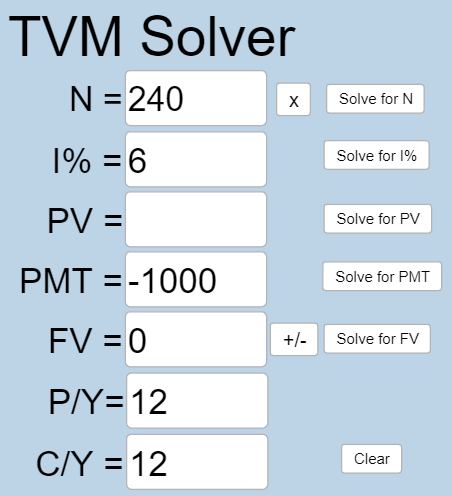
[latex]PV=139580.77[/latex], so you will need to have $139580.77 in the account when you retire.

Using the interest formula, we find that [latex]\text{Interest}=240 \times 1000-139580.77 =100419.23[/latex]. This means that the interest earned in this account is $100,419.23.
To return to Section 4.3, click here.
You know you will have $500,000 in your account when you retire. You want to be able to take monthly withdrawals from the account for a total of 30 years. Your retirement account earns 8% interest. How much will you be able to withdraw each month?
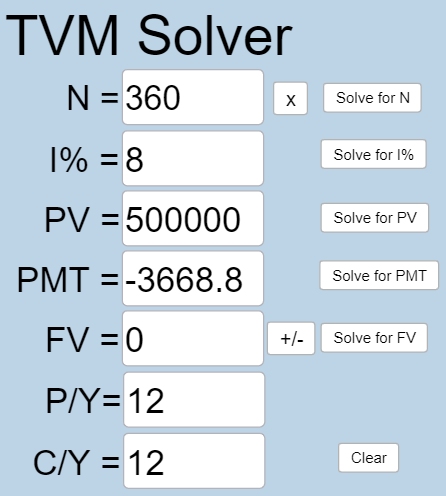
[latex]N = 30 \times 12 = 360[/latex] because you are taking making monthly withdrawals for 30 years.
[latex]I\% = 8[/latex] because the interest rate is 8%.
[latex]PV=500000[/latex] because you start with $500,000 in the account when you retire.
[latex]PMT[/latex] is what you want to know.
[latex]FV = 0[/latex] because after you’ve made all withdrawals, the account has no money in it.
[latex]P/Y=12[/latex] because you are making 12 withdrawals per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for PMT}\\ \hline \end{array}\;[/latex] button.
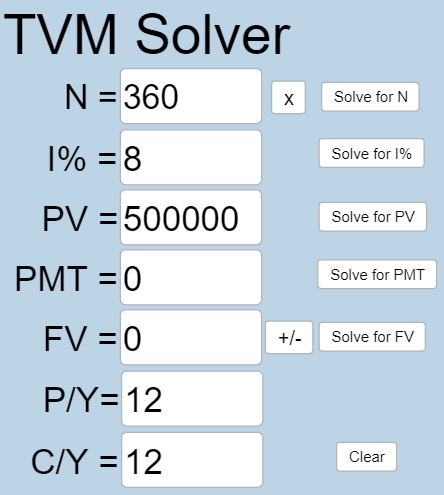
[latex]PMT=3668.82[/latex], so you would be able to withdraw $3,668.82 each month for 30 years.
To return to Section 4.3, click here.
Examples from Section 4.4
You can afford $200 per month as a car payment. If you can get an auto loan at 3% interest for 60 months (5 years), how expensive of a car can you afford? In other words, what amount loan can you pay off with $200 per month?
[latex]N =60[/latex] because the auto loan is a 60 month loan.
[latex]I\% = 3[/latex] because the interest rate is 3%.
[latex]PV[/latex] is what you want to know.
[latex]PMT=-200[/latex] because you can afford car payments of $200.
[latex]FV = 0[/latex] because after you’ve made all payments, you owe no money on the car.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for PV}\\ \hline \end{array}\;[/latex] button.
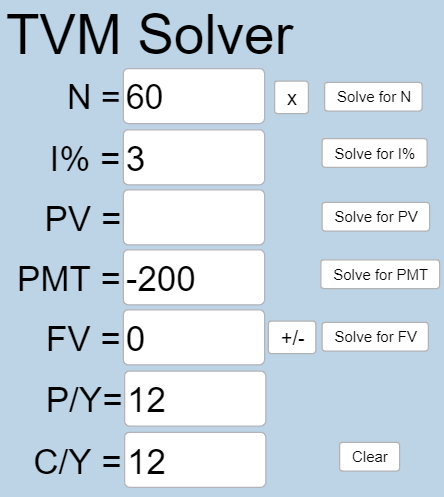
You can afford a $11,130.47 auto loan.
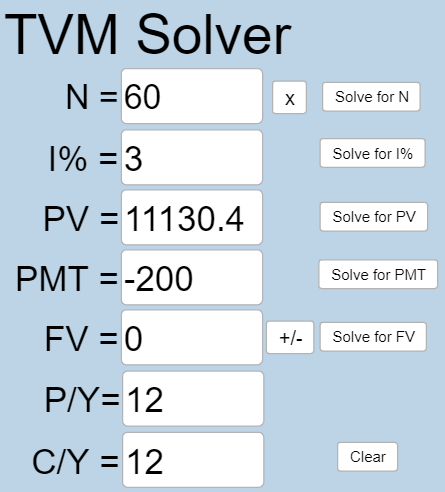
Using our interest formula, we can figure out how much interest you will have to pay.
[latex]\text{Interest}=60 \times 200-11130.47 =869.53[/latex], so you will pay $869.53 in interest.
To return to Section 4.4, click here.
You want to take out a $140,000 mortgage (home loan). The interest rate on the loan is 6%, and the loan is for 30 years. How much will your monthly payments be?
[latex]N =30 \times 12 = 360[/latex] because you will make monthly payments for 30 years.
[latex]I\% = 6[/latex] because the interest rate is 6%.
[latex]PV=140000[/latex] because you will owe $140,000 when you take out the loan.
[latex]PMT[/latex] is what you want to know.
[latex]FV = 0[/latex] because after you’ve made all payments, you owe no money on the home.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for PMT}\\ \hline \end{array}\;[/latex] button.
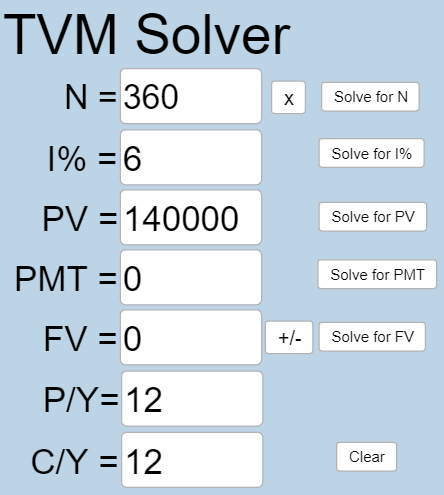
You can afford payments of $839.37.

Using our interest formula, we can figure out how much interest you will have to pay.
[latex]\text{Interest}=360 \times 839.37-140000=162173.2[/latex], so you will pay $162,173.20 in interest.
To return to Section 4.4, click here.
Consider the $140,000 mortgage at 6% from the previous example. If the homeowner increased their payments to $1000 per month, how long will it take them to pay off the loan?
[latex]N[/latex] is what you want to know.
[latex]I\% = 6[/latex] because the interest rate is 6%.
[latex]PV=140000[/latex] because the homeowner will owe $140,000 when you take out the loan.
[latex]PMT=-1000[/latex] because the homeowner will make payments of $1000.
[latex]FV = 0[/latex] because after the homeowner has made all payments, no money is owed on the mortgage.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for N}\\ \hline \end{array}\;[/latex] button.
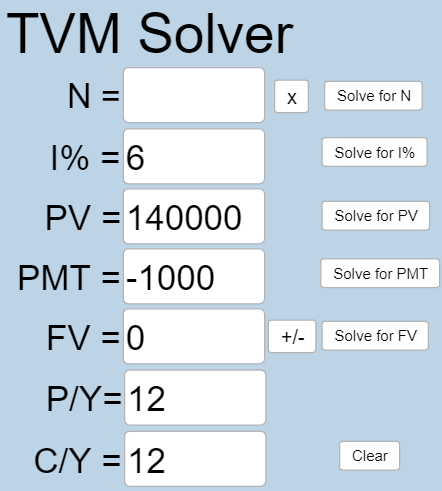
[latex]N=241.4[/latex], so it will take 241.4 months to pay off the mortgage with payments of $1000. To convert this to years, we can use a conversion factor.
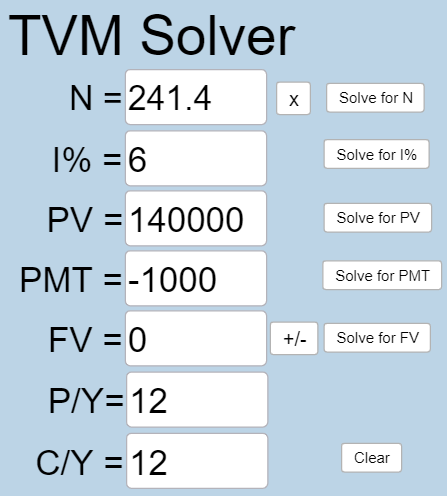
[latex]241.4 \text{ months} \times \frac{1 \text{ year}}{12 \text{ months}} \approx 20.12[/latex] years.
To return to Section 4.4, click here.
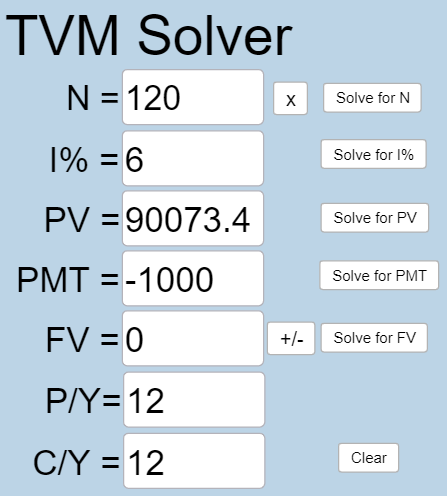
If a mortgage at a 6% interest rate has payments of $1,000 a month, how much will the loan balance be 10 years from the end the loan?
[latex]N =10 \times 12[/latex] because the monthly payments will be made for 10 years.
[latex]I\% = 6[/latex] because the interest rate is 6%.
[latex]PV[/latex] is what you want to know.
[latex]PMT=-1000[/latex] because you can afford payments of $1000.
[latex]FV = 0[/latex] because after you’ve made all payments, you owe no money on the car.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for PV}\\ \hline \end{array}\;[/latex] button.
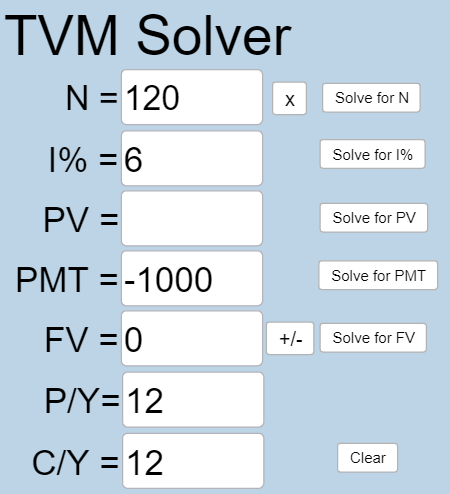
[latex]PV=90073.45[/latex], so 10 years from the end of the loan, there will be a balance of $90,073.45.
To return to Section 4.4, click here.
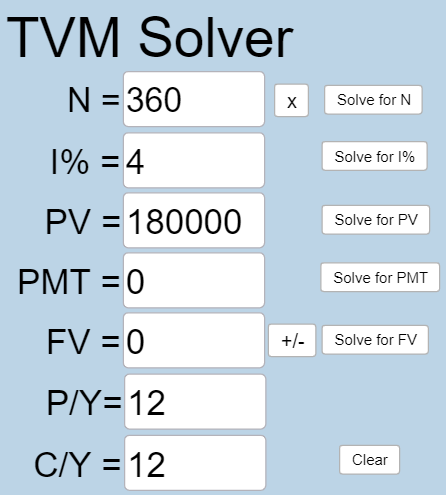
A couple purchases a home with a $180,000 mortgage at 4% for 30 years with monthly payments. What will the remaining balance on their mortgage be after 5 years?
First we will calculate the monthly payment amount.
[latex]N =30 \times 12 = 360[/latex] because they will make monthly payments for 30 years.
[latex]I\% = 4[/latex] because the interest rate is 4%.
[latex]PV=180000[/latex] because they will owe $180,000 when they take out the mortgage loan.
[latex]PMT[/latex] is what we want to know.
[latex]FV = 0[/latex] because after they’ve made all payments, they owe no money on the home.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for PMT}\\ \hline \end{array}\;[/latex] button.
The couple can afford payments of $859.35.
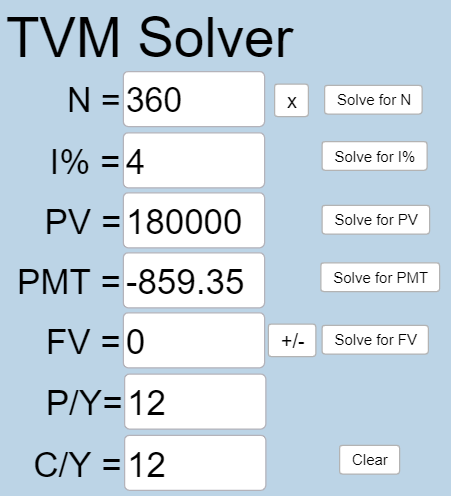
Now that we know the monthly payments, we can determine the remaining balance. We want the remaining balance after 5 years, when 25 years will be remaining on the loan, so we calculate the loan balance that will be paid off with the monthly payments over those 25 years.
[latex]N =25 \times 12[/latex] because we want to know the balance on the mortgage for the last 25 years.
[latex]I\% = 4[/latex] because the interest rate is 4%.
[latex]PV[/latex] is what we want to know.
[latex]PMT=-859.35[/latex] because the couple can afford payments of $859.35.
[latex]FV = 0[/latex] because after they’ve made all payments, they owe no money on the home.
[latex]P/Y=12[/latex] because you are making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
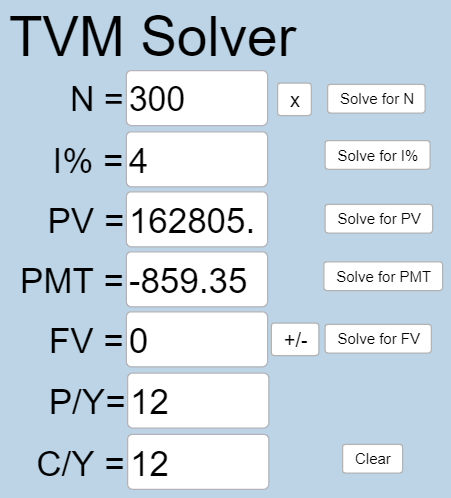
Plug all values into the TVM Solver, and click the [latex]\begin{array}{|c|}\hline \text{Solve for PV}\\ \hline \end{array}\;[/latex] button.
The loan balance after 5 years, with 25 years remaining on the loan, will be $162,805.99.
To return to Section 4.4, click here.
Examples from Section 4.5
Jenny plans to retire at age 65, and estimates she will need $48,000 a year in retirement for 30 years. To save for retirement, she plans to put money every month into her 401k plan at work. If Jenny is currently 25, how much will she need to save each month to meet her retirement goal, assuming her retirement accounts earn an average of 7% per year.
We can think about this as two separate phases: the accumulation phase and the spending phase. We assume Jenny starts with no money and the beginning, and will completely spend down her account by the time she’s 95.
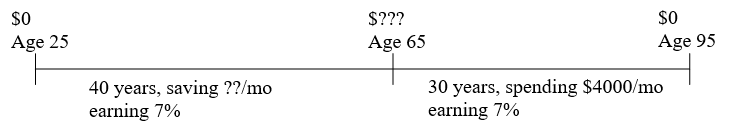
To decide which phase to start with, we look to see which we have the most information for. In the first phase, we don’t know how much she will save each month, and we don’t know the ending balance of the account. For the second phase, we know everything except the starting balance of the account, so we will start the problem in the second phase. Basically, we are going to work the problem backwards, using her spending requirement to determine how much she needs at retirement, then use that value to determine how much she needs to save each month.
The second phase is a payout annuity problem, where:
[latex]N =30 \times 12[/latex] because Jenny is saving money monthly for 30 years.
[latex]I\% = 7[/latex] because the interest rate is 7%.
[latex]PV[/latex] is what we want to know.
[latex]PMT=-4000[/latex] because Jenny is spending $4000 per month.
[latex]FV = 0[/latex] because there is no money in the account when Jenny is 95 years old.
[latex]P/Y=12[/latex] because Jenny is making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
When we solve for [latex]PV[/latex], we find that [latex]PV= $601,230.27[/latex]
This is how much Jenny will need at retirement to meet her spending needs, and fills in a part of our timeline:

Now we can work on the first phase, which is a savings annuity problem where the desired end balance is the $601,230.27 we just found.
[latex]N =40 \times 12[/latex] because Jenny is saving money monthly for 40 years.
[latex]I\% = 7[/latex] because the interest rate is 7%.
[latex]PV=0[/latex] because the account has no money in it when it is first opened.
[latex]PMT[/latex] is what we want to know.
[latex]FV=601230.27[/latex] because the account has $601230.27 in it when Jenny is 65.
[latex]P/Y=12[/latex] because Jenny is making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Using the savings annuity formula to solve for the deposit amount gives:
[latex]PMT= -229.06[/latex]
Jenny will need to save $229.06 per month to meet her retirement goals.
To return to section 4.5, click here.
Ula just got a new job. She had $70,000 in a 401k at her old job that she rolled over into an IRA. She plans to continue contributing $5,000 a year into her IRA. If her account earns 6% compounded annually, how much will she have in her IRA in 10 years?
The challenge with this problem is that our savings annuity formula assumed that our account balance started at zero. While we could try to build a new formula to handle this situation, we can more easily envision it as two different money streams, as if the original $70,000 is invested in a different account than future contributions.

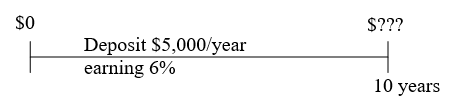
In the first stream of money, Ula has $70,000 earning 6% interest for 10 years, which is a basic compound interest problem:
[latex]P = $70,000, r = 0.06, t = 10, k = 1[/latex]
Using the compound interest formula to solve for the ending balance:
[latex]A = $125,359.34[/latex]
In the second stream of money, Ula is depositing $5,000 a year, a savings annuity problem:
[latex]N =10[/latex] because annual deposits are made into the account for 10 years.
[latex]I\% = 6[/latex] because the interest rate is 6%.
[latex]PV=0[/latex] because the account has no money in it when it is first opened.
[latex]PMT=-5000[/latex] because Ula is depositing $5,000 per year.
[latex]FV[/latex] is what we want to know.
[latex]P/Y=1[/latex] because Ula is making 1 payment per year.
[latex]C/Y=1[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Using the savings annuity formula to find the ending balance:
[latex]FV = $65,903.97[/latex]
Now that we know the ending balance of each stream of money, we can add those together to find the total balance of the account at the end of the ten years:
[latex]$125,359.34 + $65,903.97 = $191,263.31[/latex]
To return to section 4.5, click here.
Five years ago a couple purchased a home for $260,000, making a 20% down payment and financing the rest with a 30-year adjustable rate mortgage fixed at 3% for the first 5 years. Now that the fixed rate period is up, the couple is facing a higher adjustable rate. They now plan to refinance into a fixed rate 30-year mortgage at 4%. What will their new monthly payments be? Assume there are no costs associated with the refinance.
To determine the monthly payments for the refinance, we first need to know how much the refinanced loan amount will be. The amount refinanced will be the same as the remaining loan balance on the original loan after 5 years. We will start by finding the details of the original loan.
The 20% down payment will be [latex]$260,000(0.20) = $52,000[/latex], leaving $208,000 to be financed.
We start by finding the payments on the original loan:
[latex]N =30 \times 12=360[/latex] because monthly payments will be made for 30 years.
[latex]I\% = 3[/latex] because the interest rate is 3%.
[latex]PV=208000[/latex] because $208,000 needs to be financed.
[latex]PMT[/latex] is what we want to know.
[latex]FV=0[/latex] because no money is owed when the loan is paid off.
[latex]P/Y=12[/latex] because the couple is making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Solving for the payment, we get
[latex]PMT = $876.94[/latex]
Now we can find the remaining balance on the original loan after 5 years. As discussed in the last section, we can find this by determining the amount of loan that can be paid off with payments of $876.94 in the remaining 25 years:
[latex]N =25 \times 12=300[/latex] because monthly payments will be made for 25 years.
[latex]I\% = 3[/latex] because the interest rate is 3%.
[latex]PV[/latex] is what we want to know.
[latex]PMT=876.94[/latex], which we found in the first part.
[latex]FV=0[/latex] because no money is owed when the loan is paid off.
[latex]P/Y=12[/latex] because the couple is making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Solve for [latex]PV[/latex], the remaining balance,
[latex]P = $184,926.00[/latex]
So after 5 years, the remaining balance on the loan is $184,926.00, and that is the amount we will refinance in a new 30 year mortgage at the fixed 4% rate:
[latex]N =30 \times 12=360[/latex] because monthly payments will be made for 30 years.
[latex]I\% = 4[/latex] because the interest rate is 4%.
[latex]PV=184926[/latex] because $184,926 is the remaining balance after 5 years.
[latex]PMT[/latex] is what we want to know.
[latex]FV=0[/latex] because no money is owed when the loan is paid off.
[latex]P/Y=12[/latex] because the couple is making 12 payments per year.
[latex]C/Y=12[/latex] because [latex]P/Y[/latex] and [latex]C/Y[/latex] are always the same number.
Solving for the new payment amount:
[latex]PMT = $882.87[/latex]
Because of the higher interest rate the monthly payment increased, even though the loan amount was less at refinance. Most likely this increase is much smaller than the one the couple would have faced from the original loan’s rate adjusting.
Notice also that because of the refinance, the couple will end up making payments for a total of 35 years on the house.
In those first 5 years, the couple paid a total of [latex]$876.94(12)(5) = $52,616.40[/latex], and reduced the loan balance by [latex]$208,000 - $184,926 = $23,074[/latex], meaning they paid $29,542.40 in interest during the first 5 years.
In the remaining 30 years, the couple will pay [latex]$882.87(12)(30) = $317,833.20[/latex], and reduce the loan balance by $184,926, meaning they will pay $132,907.20 in interest during these 30 years.
In total, the couple will pay [latex]$132,907.20 + $29,542.40 = $162,449.60[/latex] in interest over the 35 years.
To return to section 4.5, click here.
Media Attributions
- 4.6 02 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 03 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 04 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 05 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 06 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 07 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 08 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 09 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 10 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 11 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 12 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 13 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 14 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 15 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 16
- 4.6 17 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 18 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 19 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 20 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 21 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 22 is licensed under a CC0 (Creative Commons Zero) license
- 4.6 23 is licensed under a CC0 (Creative Commons Zero) license
- 4.5 02 © Business Precalculus by David Lippman is licensed under a CC BY-SA (Attribution ShareAlike) license
- 4.5 03 © Business Precalculus by David Lippman is licensed under a CC BY-SA (Attribution ShareAlike) license
- 4.5 04 © Business Precalculus by David Lippman is licensed under a CC BY-SA (Attribution ShareAlike) license
- 4.5 05 © Business Precalculus by David Lippman is licensed under a CC BY-SA (Attribution ShareAlike) license

