Genetics of an Ear of Corn
Learning Objectives
After completing the lab, the student will be able to:
- Explain basic principles of inheritance, the definition of genotype and phenotype, and the assumptions of Mendelian inheritance.
- Use a Punnett square.
- Statistically test the probability that the difference between an observed and an expected result is due to chance.
Activity 1 Alternative: Pre-Assessment
- How would you know if a trait follows a Mendelian inheritance pattern, assuming you know and can track the genotypes and phenotypes of an organism as it produces offspring?
- What is a Punnett square, and what does it show? Using a Punnett square, predict the offspring of a cross between two heterozygous parents for gene A (Aa × Aa).
- Discuss the answers to questions 1–2 with the class.
Activity 1 Alternative: Genetics of an Ear of Corn
Photograph of corn entitled “Yellow and purple!_Gabi” by nist6ss is marked with CC BY-SA 2.0.
Activity 1: Single Trait Inheritance
Based on the principles set forth by Mendel, we can predict what genotypes and phenotypes offspring will have based on the genotypes and phenotypes of their parents. One efficient way to do this involves using a Punnett square. A Punnett square is a grid where all the alleles of one parent are provided as the column headers, while all of the alleles from the second parent are provided as the row headers (Figure 14.1). When the alleles from the two parents are combined in the grid, the internal squares predict the genotypes of their offspring. In addition, multiple Punnett squares can predict offspring genotypes across several generations. The first filial generation (F1) is the offspring that results from crossing the original, parental generation. The second filial generation (F2) is the offspring that results from crossing F1 individuals.
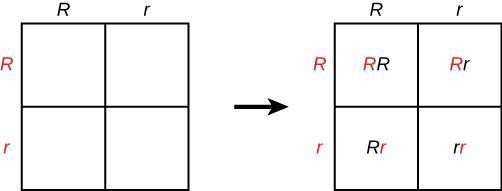
Genes of corn kernel
For color of corn kernel (purple or yellow)
For shape of corn kernel (smooth or shrunken)

Alleles of corn kernel
Alleles are versions of a gene. Dominant alleles control the appearance or phenotype of the organism. Recessive alleles disappear or recede and do not control the phenotype, unless the organisms has only recessive alleles for that gene
- Purple (P) is dominant allele
- Yellow (p) is recessive allele
- Smooth (S) is dominant allele
- Shrunken (s) is recessive allele
Phenotype of corn
Purple and smooth: 
Purple and shrunken: 
Yellow and smooth: 
Yellow and shrunken: 
Safety Precautions
- Add
For this activity, you will need the following:
- Corn cobs with different genotypes and phenotypes
- Can be acquired from commercial sources. Carolina Biological Supply and Ward’s Science are examples of companies selling corn ears for genetic studies to high schools and universities.
For this activity, you will work in pairs.
Structured Inquiry
Genotypes of corn
The corn has two parental versions of the same gene, one inherited from the female plant, the other from the male plant. For example, a corn could have Pp as a genotype for the color of the corn kernel. P from the female plant, p from the male plant. In regard to corn kernel shape, it could be SS: S from the female plant, S from the male plant.
Interactive question 1: What could be the genotype of a corn when it has a purple phenotype?
- PP only
- Pp only
- Pp or PP
- pp or PP
- pp or Pp
Interactive question 2: What could be the genotype of a corn when it has a shrunken phenotype?
- SS only
- Ss only
- Ss or SS
- ss or SS
- ss only
Homozygous means that an organism has the same allele (or version) for a gene. Heterozygous means, that an organism has different versions for an allele of the same gene. Taking the example of the corn kernel, what would a heterozygous genotype look like for the color of the corn kernel?
Interactive question 3: What would be a possible genotype for the color of a corn kernel if it would be heterozygous for color?
- PP
- pp
- Pp or pP
- All of the choices are correct
Interactive question 4: What would be a possible genotype for the shape of a corn kernel if it would be homozygous for shape?
- Ss only
- SS or ss
- SS only
- ss only
- None of the choices are correct
A corn kernel heterozygous for color and shape of the corn kernel would be PpSs.
Interactive question 5: If both parents are heterozygous and crossed for offspring, what could be the alleles of the female and male reproductive cells (gametes)?
- PS
- Ps
- pS
- ps
- all choices are possible genotypes that female and male reproductive cells (gametes) donate.
A Punnett square allows visualization of the genotypes of the parents and possible genotypes of the offspring.
Interactive question 6: What is the Punnett square for the cross of PpSs with PpSs?
Fill in the possible genotypes for the gametes
| Gametes |
|
|
|
|
|
|
||||
|
|
||||
|
|
||||
|
|
Interactive question 7: What is a correct Punnett square for the crossing mentioned above?
A)
| Gametes |
p |
s |
S |
p |
|
P |
||||
|
S |
||||
|
p |
||||
|
s |
B)
| Gametes |
pp |
Pp |
SS |
ss |
|
Pp |
||||
|
PP |
||||
|
Ss |
||||
|
ss |
C)
| Gametes |
PS |
Ps |
pS |
ps |
|
PS |
||||
|
Ps |
||||
|
pS |
||||
|
ps |
D)
| Gametes |
P |
p |
Sp |
SP |
|
Ps |
||||
|
pp |
||||
|
Sp |
||||
|
ss |
Once you have the genotypes of the gametes filled into the Punnett square, you can visualize the possible genotypes of the offspring.
Interactive question 8. Below is listed a Punnett square to be used. What would be the possible genotypes of the offspring? Spend 5 minutes to fill in the empty cells.
|
Gametes |
PS |
Ps |
pS |
ps |
|
PS |
||||
|
Ps |
||||
|
pS |
||||
|
ps |
Interactive question 9. Identify a correct Punnett square for the cross of PpSs with PpSs.
A)
|
Gametes |
PS |
Ps |
pS |
ps |
|
PS |
PPSS |
PsSS |
PPSS |
ppSS |
|
Ps |
ppSS |
PsPs |
ppSS |
PsPs |
|
pS |
ppSS |
PsPs |
ppSs |
PPss |
|
ps |
ssPP |
ppPP |
PpSS |
ppss |
B)
|
Gametes |
PS |
Ps |
pS |
ps |
|
PS |
PPss |
PPss |
ppSS |
ppss |
|
Ps |
PPSs |
PPSs |
PsSs |
Psss |
|
pS |
PsSS |
PsSs |
ppSS |
ppss |
|
ps |
PsSs |
Ppss |
ppss |
ppss |
C)
|
Gametes |
PS |
Ps |
pS |
ps |
|
PS |
PPSS |
PPSs |
PpSS |
PpSs |
|
Ps |
PPSs |
PPss |
PpSs |
Ppss |
|
pS |
PpSS |
PpSs |
ppSS |
ppSs |
|
ps |
PpSs |
Ppss |
ppSs |
ppss |
Using the genotypes, you can calculate the phenotypes.
|
Gametes |
PS |
Ps |
pS |
ps |
|
PS |
PPSS |
PPSs |
PpSS |
PpSs |
|
Ps |
PPSs |
PPss |
PpSs |
Ppss |
|
pS |
PpSS |
PpSs |
ppSS |
ppSs |
|
ps |
PpSs |
Ppss |
ppSs |
ppss |
The Punnett square shows a total of 16 genotypes for the possible offspring. The different genotypes are: PPSS (1), PPSs (2), PpSS (2), PpSs (4), PPss (1), Ppss (2), ppSS (1), ppSs (2) and ppss (1). Overall, there are 9 different genotypes for this cross. Mathematically the ratios are 1:2:2:4:1:2:1:2:1 for the genotypes.
One can also count the phenotypes. E.g. how many purple & smooth out of all possible 16 offspring? 9 out of 16 are purple & smooth. The information can be listed as follows:
9/16 Purple and Smooth 
3/16 Purple and Shrunken
3/16 Yellow and Smooth
1/16 Yellow and Shrunken
However, to simplify matters the information for the frequency of phenotypes is normally listed in the following way: 9:3:3:1.
Mathematical calculations (algebra) can predict the phenotype ratios:
One starts for one gene or trait. E.g. Color of corn kernel: 3 P (purple) and 1 p (yellow)
Then the other gene or trait. E.g. shape of corn kernel: 3 S (smooth) and 1 s (shrunken)
Then the two traits are combined: (3P + 1p) x (3S + 1s) = 9 PS + 3PS + 3pS + 1ps
Chi Square Problem: An ear of corn has a total of 381 grains, including 215 Purple & Smooth, 80 Purple & Shrunken, 65 Yellow & Smooth, and 21 Yellow & Shrunken. These phenotypes and numbers are entered in Columns 1 and 2 of the following Table 2.
Your Tentative Hypothesis: This ear of corn was produced by a dihybrid cross (PpSs x PpSs) involving two pairs of heterozygous genes resulting in a theoretical (expected) ratio of 9:3:3:1. See dihybrid cross in Table 1.
Objective: Test your hypothesis using chi square and probability values. In order to test your hypothesis, you must fill in the columns in the following Table 2.
- For the observed number (Column 2), enter the number of each grain phenotype counted on the ear of corn.
- To calculate the observed ratio (Column 3), divide the number of each grain phenotype by 21 (the grain phenotype with the lowest number of grains).
- For the expected ratio (Column 4), use 9:3:3:1, the theoretical ratio for a dihybrid cross. The fractional ratios for these four phenotypes are 9/16, 3/16, 3/16, and 1/16.
- To calculate the expected number (Column 5), multiply the number of each grain phenotype by the expected fractional ratio for that grain phenotype.
- In the last column (Column 6), for each grain phenotype take the observed number of grains (Column 2) and subtract the expected number (Column 5), square this difference, and then divide by the expected number (Column 5). Round off to three decimal places.
- To calculate the chi square value, add up the four decimal values in the last column (Column 6).
|
Grain |
Observed |
Observed |
Expected |
Expected |
[Obs No. – Exp No.]2 |
|
Purple and |
215 |
10.23 |
9 |
381 x 9/16 = 214 |
1 ÷ 214 = 0.0048 |
|
Purple and |
80 |
3.81 |
3 |
381 x 3/16 = 71 |
81/71 = 1.1408 |
|
Yellow & and |
65 |
3.09 |
3 |
381 x 3/16 = 71 |
36/71 = 0.5070 |
|
Yellow and |
21 |
1.0 |
1 |
381 x 1/16 = 24 |
9/24 = 0.375 |
|
Total |
381 |
— |
|
Chi Square |
1.9976 |
Determine the degree of freedom
For dihybrid crosses the degree of freedom (df) is (number of phenotypes −1)
Only 4 different phenotypes were observed (purple & smooth, purple & shrunken, yellow & smooth, yellow& shrunken)
9/16 Purple and Smooth: 
3/16 Purple and Shrunken: 
3/16 Yellow and Smooth: 
1/16 Yellow and Shrunken: 
degree of freedom (df) is (number of phenotypes −1)
- df = 4-1 = 3
The degree of freedom is 3
Use your own corn cob and calculate your numbers:
Chi Square Problem: An ear of corn has a total of ___ grains, including ___ Purple & Smooth, __ Purple & Shrunken, __ Yellow & Smooth, and __ Yellow & Shrunken. These phenotypes and numbers are entered in Columns 1 and 2 of the following Table 2.
|
Grain |
Observed |
Observed |
Expected |
Expected |
[Obs No. – Exp No.]2 |
|
Purple and |
|||||
|
Purple and |
|||||
|
Yellow & and |
|||||
|
Yellow and |
|||||
|
Total |



