Test for Independence (Chi-Square Test)

Activity 2: Pre-Assessment

1. What does the chi-square test tell you?
2. Explain the difference between expected and observed data.
3. What is a null hypothesis?
4. Discuss the answers to questions 1, 2, and 3 with the class.

Activity 2: Test for Independence (Chi-Square Test)

The chi-square test is an independence test for the likelihood that an observed distribution is due to chance.

Chi-square is calculated using the following equation

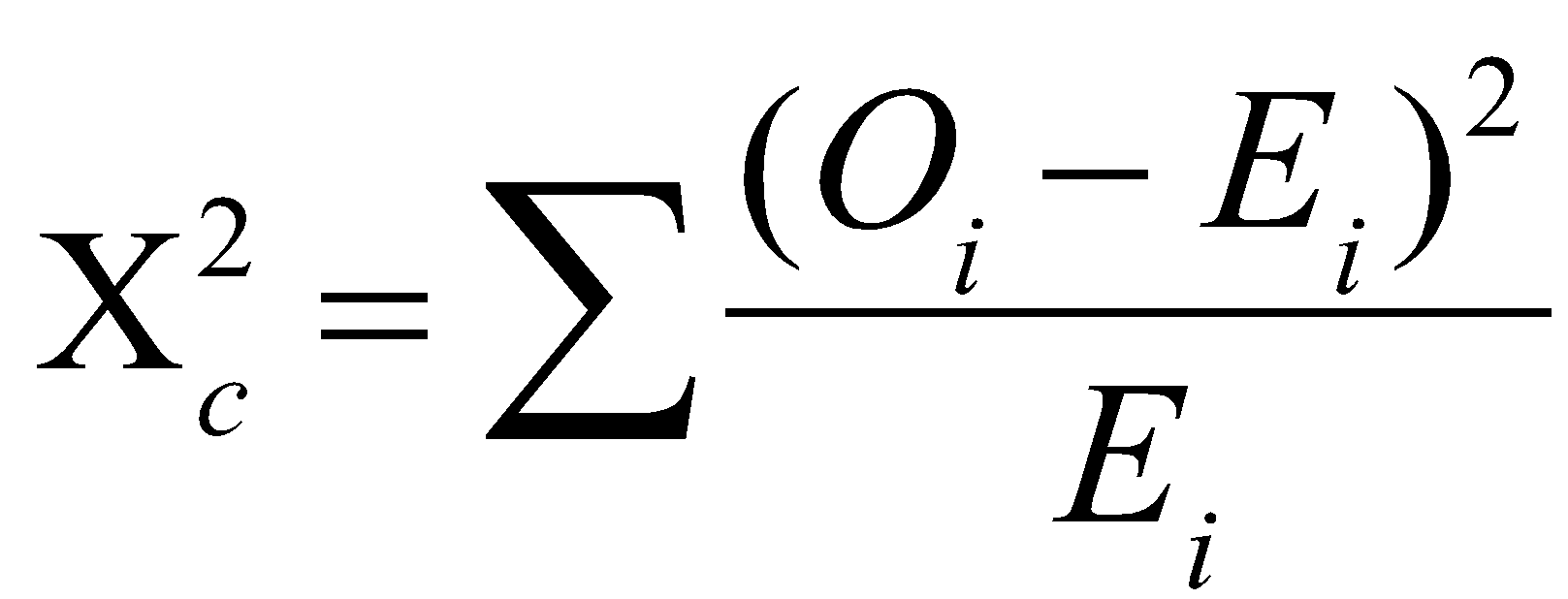
where X is the chi-square test statistic, c is the significant level of the test (we will use 0.05), O is the observed value for variable i, and E is the expected value for variable i.

To interpret the data, use a standard chi-square table, as provided by your teacher. On the left side of the table is the degree of freedom (df), which is calculated by subtracting 1 from the number of categories in the data. Across the top is the probability (p-value) or the probability that the observed value matches the expected value. It is used to determine whether the null hypothesis should be accepted or rejected. The null hypothesis states that there is no significant difference between the groups being measured.

Safety Precautions

• None

For this activity, you will need the following:

• Standard chi-square test table
• Calculator

For this activity, you will work in pairs.

Structured Inquiry

Step 1: Use chi-square analysis to determine if the data from the Activity 1 Structured Inquiry is independently assorted. Watch the video to learn how to perform a chi-square test:

Create a data table for your analysis, and show your calculations in your notebook.

Step 2: Hypothesize/Predict: Predict whether you will accept or reject your null hypothesis (i.e., if they are independently assorted). What is your alternative hypothesis? Add your predictions to the data table you created in Step 1.

Step 3: Student-Led Planning: Using the data you collected in the previous activity, perform a chi-square test. Work with your partner.

Step 4: Critical Analysis: Based on your chi-square test, will you accept or reject your hypothesis? Why or why not? What methods could you use to improve your results? Discuss with your partner, and then write your answers in your notebook.

Guided Inquiry

Step 1: Now, use chi-square analysis to determine if the data from the Activity 1 Guided Inquiry is independently assorted. Create a data table for your analysis, and show your calculations in your notebook.

Step 2: Hypothesize/Predict: Predict whether you will accept or reject your null hypothesis (i.e., are your observed results significantly different from your expected results?). What is your alternative hypothesis? Add your hypotheses to the data table you created in Step 1.

Step 3: Student-Led Planning: Using the data you collected in the previous activity, perform a chi-square test. Work with your partner. Your expected data would be the number of flies that should possess the different phenotypes based on the ratios predicted by Mendelian inheritance for each cross.

Step 4: Critical Analysis: Based on your chi-square test, will you accept or reject your hypothesis? Why or why not? What does this tell you about the validity of your data? Discuss with your partner, and then write your answers in your notebook.

Assessments

1. What does the chi-square test tell you about a set of observed versus expected results?
2. Describe another situation, outside the realm of science, where a chi-square test would be useful.
3. What would change the degree of freedom in a chi-square test?