Chapter 11: The Chi-Square Distribution
11.3 Test of Independence
Learning Objectives
By the end of this section, the student should be able to:
- calculate the test of independence and determines whether two factors are independent or not
Tests of independence involve using a contingency table of observed (data) values.
The test statistic for a test of independence is similar to that of a goodness-of-fit test: [latex]\underset{\left(i\cdot j\right)}{\Sigma }\frac{{\left(O–E\right)}^{2}}{E}[/latex] where:
- [latex]O =[/latex] observed values
- [latex]E =[/latex] expected values
- [latex]i =[/latex] the number of rows in the table
- [latex]j =[/latex] the number of columns in the table
There are [latex]i\cdot j[/latex] terms of the form [latex]\frac{{\left(O–E\right)}^{2}}{E}[/latex].
A test of independence determines whether two factors are independent or not. As a review of independence, consider the following example.
Note
The expected value for each cell needs to be at least five in order for you to use this test.
Example
Suppose [latex]A = \text{a speeding violation in the last year}[/latex] and [latex]B = \text{a cell phone user while driving}[/latex]. If [latex]A[/latex] and [latex]B[/latex] are independent then [latex]P(A \text{ and } B) = P(A)P(B)[/latex]. [latex]A \text{ and } B[/latex] is the event that a driver received a speeding violation last year and also used a cell phone while driving. Suppose, in a study of drivers who received speeding violations in the last year and who used cell phones while driving, that 755 people were surveyed. Out of the 755, 70 had a speeding violation and 685 did not; 305 used cell phones while driving and 450 did not.
Let [latex]y =[/latex] expected number of drivers who used a cell phone while driving and received speeding violations.
If [latex]A[/latex] and [latex]B[/latex] are independent, then [latex]P(A \text{ and } B) = P(A)P(B)[/latex]. By substitution, [latex]\frac{y}{755}=\left(\frac{70}{755}\right)\left(\frac{305}{755}\right)[/latex].
Solve for [latex]y[/latex]: [latex]y = \frac{\left(70\right)\left(305\right)}{755}=28.3[/latex]
About 28 people from the sample are expected to use cell phones while driving and to receive speeding violations.
In a test of independence, we state the null and alternative hypotheses in words. Since the contingency table consists of two factors, the null hypothesis states that the factors are independent and the alternative hypothesis states that they are not independent (dependent). If we do a test of independence using the example, then the null hypothesis is:
[latex]H_0:[/latex] Being a cell phone user while driving and receiving a speeding violation are independent events.
If the null hypothesis were true, we would expect about 28 people to use cell phones while driving and to receive a speeding violation.
The test of independence is always right-tailed because of the calculation of the test statistic. If the expected and observed values are not close together, then the test statistic is very large and way out in the right tail of the chi-square curve, as it is in a goodness-of-fit.
The number of degrees of freedom for the test of independence is:
[latex]df = (\text{number of columns} - 1)(\text{number of rows} - 1)[/latex]
The following formula calculates the expected number ([latex]E[/latex]):
[latex]E=\frac{\text{(row total)(column total)}}{\text{total number surveyed}}[/latex]
Your Turn!
A sample of 300 students is taken. Of the students surveyed, 50 were music students, while 250 were not. Ninety-seven were on the honor roll, while 203 were not. If we assume being a music student and being on the honor roll are independent events, what is the expected number of music students who are also on the honor roll?
Solution
About 16 students are expected to be music students and on the honor roll.
Example
In a volunteer group, adults 21 and older volunteer from one to nine hours each week to spend time with a disabled senior citizen. The program recruits among community college students, four-year college students, and nonstudents. The table below shows a sample of the adult volunteers and the number of hours they volunteer per week.
| Type of Volunteer | 1–3 Hours | 4–6 Hours | 7–9 Hours | Row Total |
|---|---|---|---|---|
| Community College Students | 111 | 96 | 48 | 255 |
| Four-Year College Students | 96 | 133 | 61 | 290 |
| Nonstudents | 91 | 150 | 53 | 294 |
| Column Total | 298 | 379 | 162 | 839 |
Is the number of hours volunteered independent of the type of volunteer?
Solution
The observed table and the question at the end of the problem, “Is the number of hours volunteered independent of the type of volunteer?” tell you this is a test of independence. The two factors are number of hours volunteered and type of volunteer. This test is always right-tailed.
[latex]H_0:[/latex] The number of hours volunteered is independent of the type of volunteer.
[latex]H_a:[/latex] The number of hours volunteered is dependent on the type of volunteer.
The expected results are in the following table.
| Type of Volunteer | 1-3 Hours | 4-6 Hours | 7-9 Hours |
|---|---|---|---|
| Community College Students | 90.57 | 115.19 | 49.24 |
| Four-Year College Students | 103.00 | 131.00 | 56.00 |
| Nonstudents | 104.42 | 132.81 | 56.77 |
For example, the calculation for the expected frequency for the top left cell is [latex]E=\frac{\left(\text{row total}\right)\left(\text{column total}\right)}{\text{total number surveyed}}=\frac{\left(255\right)\left(298\right)}{839}=90.57[/latex]
Calculate the test statistic: [latex]\chi^2 = 12.99[/latex] (You can find this using your calculator or computer.)
Distribution for the test: [latex]{\chi }_{4}^{2}[/latex]
[latex]df = (3 \text{columns} – 1)(3 \text{rows} – 1) = (2)(2) = 4[/latex]
Graph:
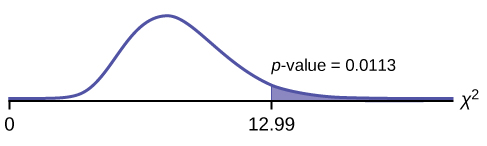
Probability statement: [latex]\text{p-value} = P(\chi^2 > 12.99) = 0.0113[/latex]
Compare [latex]\alpha[/latex] and the p-value: Since no [latex]\alpha[/latex] is given, assume [latex]\alpha = 0.05[/latex]. [latex]\text{p-value} = 0.0113[/latex], so [latex]\alpha > \text{p-value}[/latex].
Make a decision: Since [latex]\alpha > p-value[/latex], reject [latex]H_0[/latex]. This means that the factors are not independent.
Conclusion: At a 5% level of significance, from the data, there is sufficient evidence to conclude that the number of hours volunteered and the type of volunteer are dependent on one another.
For the example in the expected results table, if there had been another type of volunteer, teenagers, what would the degrees of freedom be?
Press the MATRX key and arrow over to EDIT. Press 1:[A]. Press 3 ENTER 3 ENTER. Enter the table values by row from the expected results table. Press ENTER after each. Press 2nd QUIT. Press STAT and arrow over to TESTS. Arrow down to C:χ2-TEST. Press ENTER. You should see Observed:[A] and Expected:[B]. Arrow down to Calculate. Press ENTER. The test statistic is 12.9909 and the p-value = 0.0113. Do the procedure a second time, but arrow down to Draw instead of calculate.
Your Turn!
The Bureau of Labor Statistics gathers data about employment in the United States. A sample is taken to calculate the number of U.S. citizens working in one of several industry sectors over time. The table below shows the results:
| Industry Sector | 2000 | 2010 | 2020 | Total |
|---|---|---|---|---|
| Nonagriculture wage and salary | 13,243 | 13,044 | 15,018 | 41,305 |
| Goods-producing, excluding agriculture | 2,457 | 1,771 | 1,950 | 6,178 |
| Services-providing | 10,786 | 11,273 | 13,068 | 35,127 |
| Agriculture, forestry, fishing, and hunting | 240 | 214 | 201 | 655 |
| Nonagriculture self-employed and unpaid family worker | 931 | 894 | 972 | 2,797 |
| Secondary wage and salary jobs in agriculture and private household industries | 14 | 11 | 11 | 36 |
| Secondary jobs as a self-employed or unpaid family worker | 196 | 144 | 152 | 492 |
| Total | 27,867 | 27,351 | 31,372 | 86,590 |
We want to know if the change in the number of jobs is independent of the change in years. State the null and alternative hypotheses and the degrees of freedom.
Solution
[latex]H_0:[/latex] The number of jobs is independent of the year.
[latex]H_a:[/latex] The number of jobs is dependent on the year.
[latex]df = 12[/latex]

Press the MATRX key and arrow over to EDIT. Press 1:[A]. Press 3 ENTER 3 ENTER. Enter the table values by row. Press ENTER after each. Press 2nd QUIT. Press STAT and arrow over to TESTS. Arrow down to C:χ2-TEST. Press ENTER. You should see Observed:[A] and Expected:[B]. Arrow down to Calculate. Press ENTER. The test statistic is 227.73 and the p−value = 5.90E – 42 = 0. Do the procedure a second time but arrow down to Draw instead of calculate.
Example
De Anza College is interested in the relationship between anxiety level and the need to succeed in school. A random sample of 400 students took a test that measured anxiety level and the need to succeed in school. The following table shows the results. De Anza College wants to know if anxiety level and need to succeed in school are independent events.
| Need to Succeed in School | High
Anxiety |
Med-high
Anxiety |
Medium
Anxiety |
Med-low
Anxiety |
Low
Anxiety |
Row Total |
|---|---|---|---|---|---|---|
| High Need | 35 | 42 | 53 | 15 | 10 | 155 |
| Medium Need | 18 | 48 | 63 | 33 | 31 | 193 |
| Low Need | 4 | 5 | 11 | 15 | 17 | 52 |
| Column Total | 57 | 95 | 127 | 63 | 58 | 400 |
a. How many high anxiety level students are expected to have a high need to succeed in school?
Solution
The column total for a high anxiety level is 57. The row total for high need to succeed in school is 155. The sample size or total surveyed is 400.
[latex]E=\frac{\text{(row total)(column total)}}{\text{total surveyed}}=\frac{155\cdot 57}{400}=22.09[/latex]
The expected number of students who have a high anxiety level and a high need to succeed in school is about 22.
b. If the two variables are independent, how many students do you expect to have a low need to succeed in school and a med-low level of anxiety?
Solution
The column total for a med-low anxiety level is 63. The row total for a low need to succeed in school is 52. The sample size or total surveyed is 400.
c. [latex]E=\frac{\text{(row total)(column total)}}{\text{total surveyed}} = \underline{\hspace{2cm}}[/latex]
Solution
[latex]E=\frac{\text{(row total)(column total)}}{\text{total surveyed}}=8.19[/latex]
d. The expected number of students who have a med-low anxiety level and a low need to succeed in school is about [latex]\underline{\hspace{2cm}}[/latex].
Solution
8
Your Turn!
Refer back to the information in the previous example. How many service providing jobs are there expected to be in 2020? How many nonagriculture wage and salary jobs are there expected to be in 2020?
Solution
12,727; 14,965
Section 11.3 Review
To assess whether two factors are independent or not, you can apply the test of independence that uses the chi-square distribution. The null hypothesis for this test states that the two factors are independent. The test compares observed values to expected values. The test is right-tailed. Each observation or cell category must have an expected value of at least 5.
Formula Review
- Test of Independence
- [latex]degrees of freedom = (\text{number of columns} - 1)(\text{number of rows} - 1)[/latex]
- The test statistic is [latex]\underset{\left(i\cdot j\right)}{\Sigma }\frac{{\left(O–E\right)}^{2}}{E}[/latex] where:
- [latex]O=[/latex] observed values
- [latex]E=[/latex] expected values
- [latex]i=[/latex] the number of rows in the table
- [latex]j=[/latex] the number of columns in the table
- If the null hypothesis is true, the expected number [latex]E=\frac{\text{(row total)(column total)}}{\text{total surveyed}}[/latex].
Section 11.3 Practice
Determine the appropriate test to be used in the next three exercises.
1. A pharmaceutical company is interested in the relationship between age and presentation of symptoms for a common viral infection. A random sample is taken of 500 people with the infection across different age groups.
Solution
a test of independence
2. The owner of a baseball team is interested in the relationship between player salaries and team winning percentage. He takes a random sample of 100 players from different organizations.
3. A marathon runner is interested in the relationship between the brand of shoes runners wear and their run times. She takes a random sample of 50 runners and records their run times as well as the brand of shoes they were wearing.
Solution
a test of independence
Use the following information to answer the next seven exercises: Transit Railroads is interested in the relationship between travel distance and the ticket class purchased. A random sample of 200 passengers is taken. The table below shows the results. The railroad wants to know if a passenger’s choice in ticket class is independent of the distance they must travel.
| Traveling Distance | Third class | Second class | First class | Total |
|---|---|---|---|---|
| 1–100 miles | 21 | 14 | 6 | 41 |
| 101–200 miles | 18 | 16 | 8 | 42 |
| 201–300 miles | 16 | 17 | 15 | 48 |
| 301–400 miles | 12 | 14 | 21 | 47 |
| 401–500 miles | 6 | 6 | 10 | 22 |
| Total | 73 | 67 | 60 | 200 |
1. State the hypotheses.
[latex]H_0: \underline{\hspace{2cm}}; H_a: \underline{\hspace{2cm}}[/latex]
2. [latex]df = \underline{\hspace{2cm}}[/latex]
Solution
8
3. How many passengers are expected to travel between 201 and 300 miles and purchase second-class tickets?
4. How many passengers are expected to travel between 401 and 500 miles and purchase first-class tickets?
Solution
6.6
5. What is the test statistic?
6. What is the p-value?
Solution
0.0435
7. What can you conclude at the 5% level of significance?
For each of the following problems, use the chi-square solution sheet in Chapter 11 Introduction. Round expected frequency to two decimal places.
A recent debate about where in the United States skiers believe the skiing is best prompted the following survey. Test to see if the best ski area is independent of the level of the skier.
| U.S. Ski Area | Beginner | Intermediate | Advanced |
|---|---|---|---|
| Tahoe | 20 | 30 | 40 |
| Utah | 10 | 30 | 60 |
| Colorado | 10 | 40 | 50 |
Car manufacturers are interested in whether there is a relationship between the size of car an individual drives and the number of people in the driver’s family (that is, whether car size and family size are independent). To test this, suppose that 800 car owners were randomly surveyed with the results in the table below. Conduct a test of independence.
| Family Size | Sub & Compact | Mid-size | Full-size | Van & Truck |
|---|---|---|---|---|
| 1 | 20 | 35 | 40 | 35 |
| 2 | 20 | 50 | 70 | 80 |
| 3–4 | 20 | 50 | 100 | 90 |
| 5+ | 20 | 30 | 70 | 70 |
Solution
a. [latex]H_0:[/latex] Car size is independent of family size.
b. [latex]H_a:[/latex] Car size is dependent on family size.
c. [latex]df = 9[/latex]
d. chi-square distribution with [latex]df = 9[/latex]
e. test statistic = 15.8284
f. p-value = 0.0706
g. Check student’s solution.
h. i. Alpha: 0.05
ii. Decision: Do not reject the null hypothesis.
iii. Reason for decision: p-value > alpha
iv. Conclusion: At the 5% significance level, there is insufficient evidence to conclude that car size and family size are dependent.
College students may be interested in whether or not their majors have any effect on starting salaries after graduation. Suppose that 300 recent graduates were surveyed as to their majors in college and their starting salaries after graduation. The following table shows the data. Conduct a test of independence.
| Major | < $50,000 | $50,000 – $68,999 | @69,000 + |
|---|---|---|---|
| English | 5 | 20 | 5 |
| Engineering | 10 | 30 | 60 |
| Nursing | 10 | 15 | 15 |
| Business | 10 | 20 | 30 |
| Psychology | 20 | 30 | 20 |
Some travel agents claim that honeymoon hot spots vary according to age of the bride. Suppose that 280 recent brides were interviewed as to where they spent their honeymoons. The information is given in the table below. Conduct a test of independence.
| Location | 20–29 | 30–39 | 40–49 | 50 and over |
|---|---|---|---|---|
| Niagara Falls | 15 | 25 | 25 | 20 |
| Poconos | 15 | 25 | 25 | 10 |
| Europe | 10 | 25 | 15 | 5 |
| Virgin Islands | 20 | 25 | 15 | 5 |
Solution
a. [latex]H_0:[/latex] Honeymoon locations are independent of bride’s age.
b. [latex]H_a:[/latex] Honeymoon locations are dependent on bride’s age.
c. [latex]df = 9[/latex]
d. chi-square distribution with [latex]df = 9[/latex]
e. test statistic = 15.7027
f. p-value = 0.0734
g. Check student’s solution.
h. i. Alpha: 0.05
ii. Decision: Do not reject the null hypothesis.
iii. Reason for decision: p-value > alpha
iv. Conclusion: At the 5% significance level, there is insufficient evidence to conclude that honeymoon location and bride age are dependent.
A manager of a sports club keeps information concerning the main sport in which members participate and their ages. To test whether there is a relationship between the age of a member and his or her choice of sport, 643 members of the sports club are randomly selected. Conduct a test of independence.
| Sport | 18 – 25 | 26 – 30 | 31 – 40 | 41 and over |
|---|---|---|---|---|
| racquetball | 42 | 58 | 30 | 46 |
| tennis | 58 | 76 | 38 | 65 |
| swimming | 72 | 60 | 65 | 33 |
A major food manufacturer is concerned that the sales for its skinny french fries have been decreasing. As a part of a feasibility study, the company conducts research into the types of fries sold across the country to determine if the type of fries sold is independent of the area of the country. The results of the study are shown in the following table. Conduct a test of independence.
| Type of Fries | Northeast | South | Central | West |
|---|---|---|---|---|
| skinny fries | 70 | 50 | 20 | 25 |
| curly fries | 100 | 60 | 15 | 30 |
| steak fries | 20 | 40 | 10 | 10 |
Solution
a. [latex]H_0:[/latex] The types of fries sold are independent of the location.
b. [latex]H_a:[/latex] The types of fries sold are dependent on the location.
c. [latex]df = 6[/latex]
d. chi-square distribution with [latex]df = 6[/latex]
e. test statistic =18.8369
f. p-value = 0.0044
g. Check student’s solution.
h. i. Alpha: 0.05
ii. Decision: Reject the null hypothesis.
iii. Reason for decision: p-value < alpha
iv. Conclusion: At the 5% significance level, There is sufficient evidence that types of fries and location are dependent.
According to Dan Lenard, an independent insurance agent in the Buffalo, N.Y. area, the following is a breakdown of the amount of life insurance purchased by males in the following age groups. He is interested in whether the age of the male and the amount of life insurance purchased are independent events. Conduct a test for independence.
| Age of Males | None | < $200,000 | $200,000–$400,000 | $401,001–$1,000,000 | $1,000,001+ |
|---|---|---|---|---|---|
| 20–29 | 40 | 15 | 40 | 0 | 5 |
| 30–39 | 35 | 5 | 20 | 20 | 10 |
| 40–49 | 20 | 0 | 30 | 0 | 30 |
| 50+ | 40 | 30 | 15 | 15 | 10 |
Suppose that 600 thirty-year-olds were surveyed to determine whether or not there is a relationship between the level of education an individual has and salary. Conduct a test of independence.
| Annual Salary | Not a high school graduate | High school graduate | College graduate | Masters or doctorate |
|---|---|---|---|---|
| < $30,000 | 15 | 25 | 10 | 5 |
| $30,000–$40,000 | 20 | 40 | 70 | 30 |
| $40,000–$50,000 | 10 | 20 | 40 | 55 |
| $50,000–$60,000 | 5 | 10 | 20 | 60 |
| $60,000+ | 0 | 5 | 10 | 150 |
Solution
a. [latex]H_0:[/latex] Salary is independent of level of education.
b. [latex]H_a:[/latex] Salary is dependent on level of education.
c. [latex]df = 12[/latex]
d. chi-square distribution with [latex]df = 12[/latex]
e. test statistic = 255.7704
f. p-value = 0
g. Check student’s solution.
h. i. Alpha: 0.05
ii. Decision: Reject the null hypothesis.
iii. Reason for decision: p-value < alpha
iv. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that salary and level of education are dependent.
Read the statement and decide whether it is true or false.
1. The number of degrees of freedom for a test of independence is equal to the sample size minus one.
2. The test for independence uses tables of observed and expected data values.
Solution
true
3. The test to use when determining if the college or university a student chooses to attend is related to his or her socioeconomic status is a test for independence.
4. In a test of independence, the expected number is equal to the row total multiplied by the column total divided by the total surveyed.
Solution
true
An ice cream maker performs a nationwide survey about favorite flavors of ice cream in different geographic areas of the U.S. Based on the table below, do the numbers suggest that geographic location is independent of favorite ice cream flavors? Test at the 5% significance level.
| U.S. region/Flavor | Strawberry | Chocolate | Vanilla | Rocky Road | Mint Chocolate Chip | Pistachio | Row total |
|---|---|---|---|---|---|---|---|
| West | 12 | 21 | 22 | 19 | 15 | 8 | 97 |
| Midwest | 10 | 32 | 22 | 11 | 15 | 6 | 96 |
| East | 8 | 31 | 27 | 8 | 15 | 7 | 96 |
| South | 15 | 28 | 30 | 8 | 15 | 6 | 102 |
| Column Total | 45 | 112 | 101 | 46 | 60 | 27 | 391 |
The following table provides a recent survey of the youngest online entrepreneurs whose net worth is estimated at one million dollars or more. Their ages range from 17 to 30. Each cell in the table illustrates the number of entrepreneurs who correspond to the specific age group and their net worth. Are the ages and net worth independent? Perform a test of independence at the 5% significance level.
| Age Group\ Net Worth Value (in millions of US dollars) | 1–5 | 6–24 | ≥25 | Row Total |
|---|---|---|---|---|
| 17–25 | 8 | 7 | 5 | 20 |
| 26–30 | 6 | 5 | 9 | 20 |
| Column Total | 14 | 12 | 14 | 40 |
Solution
a. [latex]H_0:[/latex] Age is independent of the youngest online entrepreneurs’ net worth.
b. [latex]H_a:[/latex] Age is dependent on the net worth of the youngest online entrepreneurs.
c. [latex]df = 2[/latex]
d. chi-square distribution with [latex]df = 2[/latex]
e. test statistic = 1.76
f. p-value 0.4144
g. Check student’s solution.
h. i. Alpha: 0.05
ii. Decision: Do not reject the null hypothesis.
iii. Reason for decision: p-value > alpha
iv. Conclusion: At the 5% significance level, there is insufficient evidence to conclude that age and net worth for the youngest online entrepreneurs are dependent.
A 2013 poll in California surveyed people about taxing sugar-sweetened beverages. The results are presented in the table below, and are classified by ethnic group and response type. Are the poll responses independent of the participants’ ethnic group? Conduct a test of independence at the 5% significance level.
| Opinion/Ethnicity | Asian-American | White/Non-Hispanic | African-American | Latino | Row Total |
|---|---|---|---|---|---|
| Against tax | 48 | 433 | 41 | 160 | 628 |
| In Favor of tax | 54 | 234 | 24 | 147 | 459 |
| No opinion | 16 | 43 | 16 | 19 | 84 |
| Column Total | 118 | 710 | 71 | 272 | 1171 |
References
DiCamilo, Mark, Mervin Field. “Most Californians See a Direct Linkage between Obesity and Sugary Sodas. Two in Three Voters Support Taxing Sugar-Sweetened Beverages If Proceeds Are Tied to Improving School Nutrition and Physical Activity Programs.” The Field Poll, released Feb. 14, 2013. Available online at http://field.com/fieldpollonline/subscribers/Rls2436.pdf (accessed May 24, 2013).
Harris Interactive. “Favorite Flavor of Ice Cream.” Available online at http://www.statisticbrain.com/favorite-flavor-of-ice-cream (accessed May 24, 2013)
“Youngest Online Entrepreneurs List.” Available online at http://www.statisticbrain.com/youngest-online-entrepreneur-list (accessed May 24, 2013).

