Chapter 3: Probability Topics
3.2 Independent and Mutually Exclusive Events
Learning Objectives
By the end of this section, you should be able to:
- Identify two events as mutually exclusive, or not
- Identify two events as independent, or not
- Use the relationships between events to compute probabilities
Often we are not just interested in a single event, but multiple events happening at the same time. In order to find probabilities relating to multiple events, we first have to know about the relationship (or lack thereof) between them. The two main relationship terms we will look for are independence and mutually exclusive. Remember, these two terms do not mean the same thing, neither are they opposites.
Independent Events
Two events A and B are independent if the knowledge that one occurred does not affect the chance the other occurs. For example, the outcomes of two rolls of a fair die are independent events, because the outcome of the first roll does not change the probability for the outcome of the second roll. If two events are NOT independent, then we say that they are dependent.
Two events are independent if and only if all of the following are true:
- [latex]P(A | B) = P(A)[/latex]
- [latex]P(B | A ) = P(B)[/latex]
- [latex]P(A \text{ AND } B) = P(A \cap B) = P(A) P(B).[/latex]
So to show two events are independent, you must show just one of the above conditions holds.
How you sample can have implications on independence. Sampling may be done with replacement or without replacement.
- With replacement: If each member of a population is replaced after it is picked, then that member has the possibility of being chosen more than once. When sampling is done with replacement, then events are independent because the result of the first pick will not change the probabilities for the second pick.
- Without replacement: When sampling is done without replacement, each member of a population may be chosen only once. In this case, the probabilities for the second pick are affected by the result of the first pick. The events are dependent.
Example
You have a fair, well-shuffled deck of 52 cards. It consists of four suits. The suits are clubs, diamonds, hearts and spades. There are 13 cards in each suit consisting of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (jack), Q (queen), K (king) of that suit.
a. Sampling with replacement:
Suppose you pick three cards with replacement. The first card you pick out of the 52 cards is the Q of spades. You put this card back, reshuffle the cards and pick a second card from the 52-card deck. It is the ten of clubs. You put this card back, reshuffle the cards and pick a third card from the 52-card deck. This time, the card is the Q of spades again. Your picks are {Q of spades, ten of clubs, Q of spades}. You have picked the Q of spades twice. On each of the three draws, you pick from the full 52-card deck.
b. Sampling without replacement:
Suppose you pick three cards without replacement. The first card you pick out of the 52 cards is the K of hearts. You put this card aside and pick the second card from the 51 cards remaining in the deck. It is the three of diamonds. You put this card aside and pick the third card from the remaining 50 cards in the deck. The third card is the J of spades. Your picks are {K of hearts, three of diamonds, J of spades}. Because you have picked the cards without replacement, you cannot pick the same card twice.
Your Turn!
You have a fair, well-shuffled deck of 52 cards. It consists of four suits. The suits are clubs, diamonds, hearts and spades. There are 13 cards in each suit consisting of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (jack), Q (queen), K (king) of that suit.
- Suppose you know that the picked cards are Q of spades, K of hearts and Q of spades. Can you decide if the sampling was with or without replacement?
- Suppose you are dealt three cards for the start of a game, the Q of spades, K of hearts, and J of spades. Can you decide if the sampling was with or without replacement?
Your Turn!
You have a fair, well-shuffled deck of 52 cards. It consists of four suits. The suits are clubs, diamonds, hearts, and spades. There are 13 cards in each suit consisting of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (jack), Q (queen), and K (king) of that suit. S = spades, H = Hearts, D = Diamonds, C = Clubs. Suppose that you sample four cards without replacement. Which of the following outcomes are possible? Answer the same question for sampling with replacement.
- QS, 1D, 1C, QD
- KH, 7D, 6D, KH
- QS, 7D, 6D, KS
Solution
When drawing without replacement, the second option is not possible because the King of Hearts is repeated. When drawing with replacement, all possibilities can occur.
Mutually Exclusive Events
Events [latex]A[/latex] and [latex]B[/latex] are mutually exclusive events if they cannot occur at the same time. This means that [latex]A[/latex] and [latex]B[/latex] do not share any outcomes, [latex]A \cap B = \emptyset[/latex] where [latex]\emptyset = \{ \}[/latex] is the empty set, and [latex]P(A \text{ AND } B) = P(A \cap B) = 0[/latex].
Example
Suppose the sample space contains the integers one through ten, [latex]S = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}[/latex]. Let [latex]A= \{1, 2, 3, 4, 5\},B= \{4, 5, 6, 7, 8\}[/latex], and [latex]C = \{7, 9\}[/latex].
Then [latex]A \cap B = \{ 4, 5\}[/latex]. Furthermore, [latex]P(A \cap B) = \frac{2}{10}[/latex], which is not zero. Therefore, [latex]A[/latex] and [latex]B[/latex] are not mutually exclusive.
However, [latex]A[/latex] and [latex]C[/latex] have no numbers in common. Thus [latex]A \cap C = \emptyset[/latex] and [latex]P(A \cap C) = 0[/latex], so [latex]A[/latex] and [latex]C[/latex] are mutually exclusive.
Example
Flip two fair coins. (This is an experiment.)
The sample space is {HH, HT, TH, TT} where T = tails and H = heads. The outcomes are HH, HT, TH, and TT. The outcomes HT and TH are different. The HT means that the first coin showed heads and the second coin showed tails. The TH means that the first coin showed tails and the second coin showed heads.
- Let A = the event of getting at most one tail. (At most one tail means zero or one tail.) Then A can be written as {HH, HT, TH}. The outcome HH shows zero tails. HT and TH each show one tail.
- Let B = the event of getting all tails. B can be written as {TT}. B is the complement of A, so B = A′. Also, [latex]P(A) + P(B) = P(A) + P(A′) = 1[/latex].
- The probabilities for A and for B are [latex]P(A) = \frac{3}{4}[/latex] and [latex]P(B) = \frac{1}{4}[/latex].
- Let C = the event of getting all heads. C = {HH}. Since B = {TT}, [latex]P(B \text{ AND } C) = 0[/latex]. B and C are mutually exclusive. (B and C have no members in common because you cannot have all tails and all heads at the same time.)
- Let D = event of getting more than one tail. D = {TT}. [latex]P(D) = \frac{1}{4}[/latex]
- Let E = event of getting a head on the first roll. (This implies you can get either a head or tail on the second roll.) E = {HT, HH}. [latex]P(E) = \frac{2}{4}[/latex]
- Find the probability of getting at least one (one or two) tail in two flips. Let F = event of getting at least one tail in two flips. F = {HT, TH, TT}. [latex]P(F) = \frac{3}{4}[/latex]
Your Turn!
Draw two cards from a standard 52-card deck with replacement. Find the probability of getting at least one black card. (Half of the cards are red, half are black.)
The sample space of drawing two cards with replacement from a standard 52-card deck with respect to color is {BB,BR,RB,RR}. The event A is {BB,BR,RB}. So [latex]P(A)=\frac{3}{4}[/latex].
Your Turn!
Flip two fair coins. Find the probabilities of the events.
- Let F = the event of getting at most one tail (zero or one tail).
- Let G = the event of getting two faces that are the same.
- Let H = the event of getting a head on the first flip followed by a head or tail on the second flip.
- Are F and G mutually exclusive?
- Let J = the event of getting all tails. Are J and H mutually exclusive?
Solution
- S contains 4 outcomes, [latex]\{HH,HT,TH,TT \}[/latex]. [latex]F= \{HH,HT,TH \}[/latex].
[latex]P(F)=\frac{3}{4}[/latex] - [latex]G=\{HH,TT \}[/latex], so [latex]P(G)=\frac{2}{4}=\frac{1}{2}[/latex]
- [latex]H=\{HH,HT \}[/latex], so [latex]P(H)=\frac{1}{2}[/latex]
- No, they are not. [latex]F\cap G= \{HH \}[/latex], so [latex]P(F\cap G)=\frac{1}{4}[/latex], not 0.
- [latex]J=\{TT \}[/latex] is mutually exclusive from [latex]H=\{HH,HT \}[/latex], as [latex]J\cap H= \{ \}[/latex] and [latex]P(J \cap H)=0[/latex].
The Axioms of Probability
Finding probabilities in more complicated situations starts with the three Axioms of Probability. Two were mentioned in the previous section, and the third we can now understand.
- [latex]P(S) = 1[/latex], that is, the probability of the sample space is one.
- [latex]0 \leq P(E) \leq 1[/latex], that is, for any event [latex]E[/latex], the probability is between 0 and 1 inclusive.
- For any two mutually exclusive events [latex]E_1[/latex] and [latex]E_2[/latex], that is, [latex]E_1 \cap E_2 = \emptyset[/latex], [latex]P(E_1 \cup E_2) = P(E_1) + P(E_2)[/latex].
The first two Axioms should be fairly intuitive. Axiom 1 says that the probabilities of all outcomes in a sample space will always add up to 1. Axiom 2 says the probability of any event must be between 0 and 1. The Third Axiom is called the disjoint addition rule; if we know two events are mutually exclusive, then we can find the probability of their OR event by adding their probabilities.
Assumptions about Events
Consider two events. If it is not known whether they are mutually exclusive, assume they are not until you can show otherwise. Likewise, if it is not known whether the events are independent, assume they are dependent until you can show otherwise. This “default” starting point is illustrated by the 4th position in the following table:
| Independent? | |||
| Yes | No | ||
| Mutually Exclusive? | Yes | 1* | 2 |
| No | 3 | 4 | |
Depending on the information given in the problem and assumptions you are able to make, as you move around the above grid, you will apply slightly different versions of each important probability rule.
Note: You will rarely, if ever, find yourself in this case.
Your Turn!
Let event C = taking an English class. Let event D = taking a speech class.
Suppose [latex]P(C) = 0.75, P(D) = 0.3, P(C|D) = 0.75[/latex] and [latex]P(C \text{ AND } D) = 0.225[/latex].
Justify your answers to the following questions numerically.
- Are C and D independent?
- Are C and D mutually exclusive?
- What is [latex]P(D|C)[/latex]?
Solution
- Yes, because [latex]P(C|D) = P(C)[/latex].
- No, because [latex]P(C \text{ AND } D)[/latex] is not equal to zero.
- [latex]P(D|C) = \frac{P\text{(}C\text{ AND }D\text{)}}{P\text{(}C\text{)}}[/latex] = [latex]\frac{\text{0}\text{.225}}{0.75}[/latex] = 0.3
Your Turn!
A box has two balls, one white and one red. We select one ball, put it back in the box, and select a second ball (sampling with replacement). Find the probability of the following events:
- Let F = the event of getting the white ball twice.
- Let G = the event of getting two balls of different colors.
- Let H = the event of getting white on the first pick.
- Are F and G mutually exclusive?
- Are G and H mutually exclusive?
Solution
- [latex]P(F) = \frac{1}{4}[/latex]
- [latex]P(G) = \frac{1}{2}[/latex]
- [latex]P(H) = \frac{1}{2}[/latex]
- Yes
- No
Your Turn!
Roll one fair, six-sided die. The sample space is {1, 2, 3, 4, 5, 6}. Let event A = a face is odd. Then A = {1, 3, 5}. Let event B = a face is even. Then B = {2, 4, 6}.
- Find the complement of A, A′. The complement of A, A′, is B because A and B together make up the sample space. [latex]P(A) + P(B) = P(A) + P(A′) = 1[/latex]. Also, [latex]P(A) = \frac{3}{6}[/latex] and [latex]P(B) = \frac{3}{6}[/latex].
- Let event C = odd faces larger than two. Then C = {3, 5}. Let event D = all even faces smaller than five. Then D = {2, 4}. [latex]P(C \text{ AND } D) = 0[/latex] because you cannot have an odd and even face at the same time. Therefore, C and D are mutually exclusive events.
- Let event E = all faces less than five. E = {1, 2, 3, 4}.
Are C and E mutually exclusive events? (Answer yes or no.) Why or why not?
Solution
No. C = {3, 5} and E = {1, 2, 3, 4}. [latex]P(C \text{ AND } E) = \frac{1}{6}[/latex]. To be mutually exclusive, [latex]P(C \text{ AND } E)[/latex] must be zero.
We can also find [latex]P(C|A)[/latex], a conditional probability. Recall that the event C is {3, 5} and event A is {1, 3, 5}. To find [latex]P(C|A)[/latex], find the probability of C using the sample space A. You have reduced the sample space from the original sample space {1, 2, 3, 4, 5, 6} to {1, 3, 5}. So, [latex]P(C | A) = \frac{2}{3}[/latex].
Your Turn!
Let event G = taking a math class. Let event H = taking a science class. Then, G AND H = taking a math class and a science class. Suppose [latex]P(G) = 0.6, P(H) = 0.5,[/latex] and [latex]P(G \text{ AND } H) = 0.3[/latex]. Are G and H independent?
If G and H are independent, then you must show ONE of the following:
- [latex]P(G|H) = P(G)[/latex]
- [latex]P(H|G) = P(H)[/latex]
- [latex]P(G \text{ AND } H) = P(G)P(H)[/latex]
Note: The choice you make depends on the information you have. You could choose any of the methods here because you have the necessary information.
a. Show that [latex]P(G|H) = P(G)[/latex].
Solution
[latex]P(G|H) = \frac{P(G \text{ AND }H )}{P(H)} = \frac{0.3}{0.5}= 0.6 = P(G)[/latex]
b. Show [latex]P(G \text{ AND } H) = P(G)P(H)[/latex].
Solution
[latex]P(G)P(H) = (0.6)(0.5) = 0.3 = P(G \text{ AND } H)[/latex]
Since G and H are independent, knowing that a person is taking a science class does not change the chance that he or she is taking a math class. If the two events had not been independent (that is, they are dependent) then knowing that a person is taking a science class would change the chance he or she is taking math. For practice, show that [latex]P(H|G) = P(H)[/latex] to show that G and H are independent events.
Your Turn!
Mark is deciding which route to take to work. His choices are I = the Interstate and F = Fifth Street.
- [latex]P(I) = 0.44[/latex] and [latex]P(F) = 0.56[/latex]
- [latex]P(I \text{ AND } F) = 0[/latex] because Mark will take only one route to work.
What is the probability of [latex]P(I \text{ OR } F)[/latex]?
Solution
Because [latex]P(I \text{ AND } F) = 0, P(I \text{ OR } F) = P(I) + P(F) - P(I \text{ AND } F) = 0.44 + 0.56 - 0 = 1[/latex]
Your Turn!
In a particular college class, 60% of the students are female. Fifty percent of all students in the class have long hair. Forty-five percent of the students are female and have long hair. Of the female students, 75% have long hair. Let F be the event that a student is female. Let L be the event that a student has long hair. One student is picked randomly. Are the events of being female and having long hair independent?
- The following probabilities are given in this example:
- [latex]P(F) = 0.60; P(L) = 0.50[/latex]
- [latex]P(F \text{ AND } L) = 0.45[/latex]
- [latex]P(L|F) = 0.75[/latex]
Condition 1: Check whether [latex]P(F \text{ AND } L) = P(F)P(L)[/latex]. We are given that [latex]P(F \text{ AND } L) = 0.45[/latex], but [latex]P(F)P(L) = (0.60)(0.50) = 0.30[/latex]. The events of being female and having long hair are not independent because [latex]P(F \text{ AND } L)[/latex] does not equal [latex]P(F)P(L)[/latex].
Condition 3: Check whether [latex]P(L|F)[/latex] equals [latex]P(L)[/latex]. We are given that [latex]P(L|F) = 0.75[/latex], but [latex]P(L) = 0.50[/latex]; they are not equal. The events of being female and having long hair are not independent.
Interpretation of Results: The events of being female and having long hair are not independent; knowing that a student is female changes the probability that a student has long hair.
Your Turn!
In a basketball arena,
- 70% of the fans are rooting for the home team.
- 25% of the fans are wearing blue.
- 20% of the fans are wearing blue and are rooting for the away team.
- Of the fans rooting for the away team, 67% are wearing blue.
Let A be the event that a fan is rooting for the away team.
Let B be the event that a fan is wearing blue.
Are the events of rooting for the away team and wearing blue independent? Are they mutually exclusive?
Solution
[latex]P(B|A) = 0.67[/latex]
[latex]P(B) = 0.25[/latex]
So [latex]P(B)[/latex] does not equal [latex]P(B|A)[/latex] which means that B and A are not independent (wearing blue and rooting for the away team are not independent). They are also not mutually exclusive, because [latex]P(B \text{ AND } A) = 0.20[/latex], not 0.
Section 3.2 Review
Two events [latex]A[/latex] and [latex]B[/latex] are independent if the knowledge that one occurred does not affect the chance the other occurs. If two events are not independent, then we say that they are dependent.
In sampling with replacement, each member of a population is replaced after it is picked, so that member has the possibility of being chosen more than once, and the events are considered to be independent. In sampling without replacement, each member of a population may be chosen only once, and the events are considered not to be independent. When events do not share outcomes, they are mutually exclusive of each other.
Formula Review
If [latex]A[/latex] and [latex]B[/latex] are independent, [latex]P(A \text{ AND } B) = P(A)P(B), P(A | B) = P(A)[/latex] and [latex]P(B | A ) = P(B)[/latex]. Equivalently, [latex]P(A \cap B) = P(A)P(B)[/latex].
If [latex]A[/latex] and [latex]B[/latex] are mutually exclusive, [latex]P(A \text{ OR } B)= P(A) + P(B)[/latex] and [latex]P(A \text{ AND }B) = 0[/latex]. Equivalently, [latex]P(A \cup B) = P(A) + P(B)[/latex] and [latex]P(A \cap B) = 0[/latex] because [latex]A \cap B = \emptyset[/latex].
Section 3.2 Practice
E and F are mutually exclusive events. [latex]P(E) = 0.4; P(F) = 0.5[/latex]. Find [latex]P(E∣F)[/latex].
J and K are independent events. [latex]P(J|K) = 0.3[/latex]. Find [latex]P(J)[/latex].
Solution
[latex]P(J) = 0.3[/latex]
U and V are mutually exclusive events. [latex]P(U) = 0.26; P(V) = 0.37[/latex]. Find:
- [latex]P(U \text{ AND } V) =[/latex]
- [latex]P(U|V) =[/latex]
- [latex]P(U \text{ OR } V) =[/latex]
Q and R are independent events. [latex]P(Q) = 0.4[/latex] and [latex]P(Q \text{ AND } R) = 0.1[/latex]. Find [latex]P(R)[/latex].
Solution
[latex]P(Q \text{ AND } R) = P(Q)P(R)[/latex]
[latex]0.1 = (0.4)P(R)[/latex]
[latex]P(R) = 0.25[/latex]
Use the following information to answer the next 12 exercises. The graph shown is based on more than 170,000 interviews done by Gallup that took place from January through December 2012. The sample consists of employed Americans 18 years of age or older. The Emotional Health Index Scores are the sample space. We randomly sample one Emotional Health Index Score.
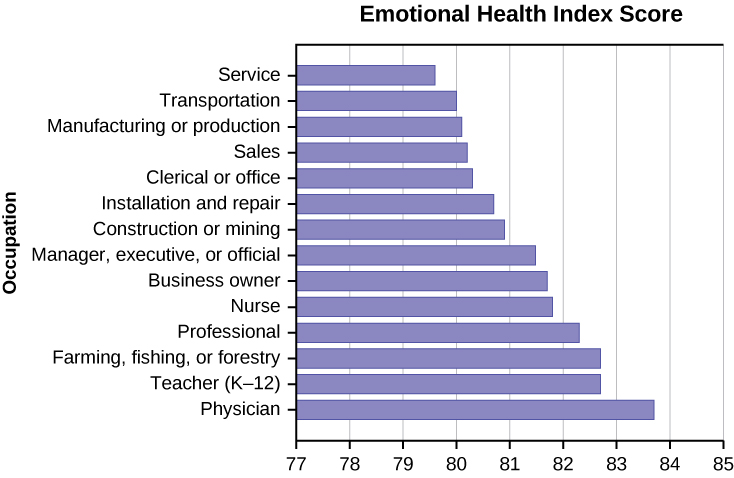
1. Find the probability that an Emotional Health Index Score is 82.7.
2. Find the probability that an Emotional Health Index Score is 81.0.
Solution
0
3. Find the probability that an Emotional Health Index Score is more than 81?
4. Find the probability that an Emotional Health Index Score is between 80.5 and 82?
Solution
0.3571
5. If we know an Emotional Health Index Score is 81.5 or more, what is the probability that it is 82.7?
6. What is the probability that an Emotional Health Index Score is 80.7 or 82.7?
Solution
0.2142
7. What is the probability that an Emotional Health Index Score is less than 80.2 given that it is already less than 81.
8. What occupation has the highest emotional index score?
Solution
Physician (83.7)
9. What occupation has the lowest emotional index score?
10. What is the range of the data?
Solution
83.7 − 79.6 = 4.1
11. Compute the average EHIS.
12. If all occupations are equally likely for a certain individual, what is the probability that he or she will have an occupation with lower than average EHIS?
Solution
[latex]P(\text{Occupation} \lt 81.3) = 0.5[/latex]
Bringing It Together
A previous year, the weights of the members of the San Francisco 49ers and the Dallas Cowboys were published in the San Jose Mercury News. The factual data are compiled into the table below.
| Shirt# | ≤ 210 | 211–250 | 251–290 | 290≤ |
|---|---|---|---|---|
| 1–33 | 21 | 5 | 0 | 0 |
| 34–66 | 6 | 18 | 7 | 4 |
| 66–99 | 6 | 12 | 22 | 5 |
Suppose that you randomly select one player from the 49ers or Cowboys. If having a shirt number from one to 33 and weighing at most 210 pounds were independent events, then what should be true about [latex]P(\text{Shirt \#} 1–33|\le 210 pounds)[/latex]?
The probability that a male develops some form of cancer in his lifetime is 0.4567. The probability that a male has at least one false positive test result (meaning the test comes back for cancer when the man does not have it) is 0.51. Some of the following questions do not have enough information for you to answer them. Write “not enough information” for those answers. Let C = a man develops cancer in his lifetime and P = man has at least one false positive.
Solution
a. [latex]P(C) = 0.4567[/latex]
b. not enough information
c. not enough information
d. No, because over half (0.51) of men have at least one false positive text
Given events G and H: [latex]P(G) = 0.43; P(H) = 0.26; P(H \text{ AND } G) = 0.14[/latex]
a. Find [latex]P(H \text{ OR } G)[/latex].
b. Find the probability of the complement of event (H AND G).
c. Find the probability of the complement of event (H OR G).
Given events J and K: [latex]P(J) = 0.18; P(K) = 0.37; P(J \text{ OR } K) = 0.45[/latex]
a. Find [latex]P(J \text{ OR } K)[/latex].
b. Find the probability of the complement of event (J AND K).
c. Find the probability of the complement of event (J AND K).
Solution
a. [latex]P(J \text{ OR } K) = P(J) + P(K) − P(J AND K); 0.45 = 0.18 + 0.37 - P(J AND K)[/latex]; solve to find [latex]P(J \text{ AND } K) = 0.10[/latex]
b. [latex]P(NOT (J \text{ AND } K)) = 1 - P(J AND K) = 1 - 0.10 = 0.90[/latex]
c. [latex]P(NOT (J \text{ OR } K)) = 1 - P(J OR K) = 1 - 0.45 = 0.55[/latex]
References
Lopez, Shane, Preety Sidhu. “U.S. Teachers Love Their Lives, but Struggle in the Workplace.” Gallup Wellbeing, 2013. http://www.gallup.com/poll/161516/teachers-love-lives-struggle-workplace.aspx (accessed May 2, 2013).
Data from Gallup. Available online at www.gallup.com/ (accessed May 2, 2013).
The occurrence of one event has no effect on the probability of the occurrence of another event. Events A and B are independent if one of the following is true:
• P(A|B) = P(A)
• P(B|A) = P(B)
• P(A AND B) = P(A)P(B)
If two events are NOT independent, then we say that they are dependent.
Once a member of the population is selected for inclusion in a sample, that member is returned to the population for the selection of the next individual.
A member of the population may be chosen for inclusion in a sample only once. If chosen, the member is not returned to the population before the next selection.
Two events are mutually exclusive if the probability that they both happen at the same time is zero. If events A and B are mutually exclusive, then P(A AND B) = 0.

