Chapter 3: Probability Topics
3.3 Two Basic Rules of Probability
Learning Objectives
By the end of this section, you should be able to:
- state and apply the multiplication rule to any two events
- state and apply the multiplication rule for independent events
- state and apply the addition rule for any two events
- state and apply the addition rule for mutually exclusive events
Recall the different combinations of relationships between two events:
| Independent? | |||
| Yes | No | ||
| Disjoint? | Yes | 1* | 2 |
| No | 3 | 4 | |
We must always go into a problem assuming two events are not mutually exclusive or independent. This "default" starting point is illustrated by the 4th position in the table above. Depending on the information you are given and assumptions you are able to make, you may move potions on this grid. Where you fall on the grid will dictate how we apply the rules we will discuss in this section to find probabilities of compound events.
There are two types of compound events we may be interested in, Unions (OR) and Intersections (AND), each with their own set of rules and assumptions. When calculating probability, there are two rules to consider when determining if the two events are independent or dependent and if they are mutually exclusive or not.
*Note: You will rarely, if ever, find yourself in this case
The Multiplication Rule
If [latex]A[/latex] and [latex]B[/latex] are two events defined on a sample space, then: [latex]P(A \text{ AND } B) = P(B) P(A|B)[/latex], or equivalently, [latex]P(A \cap B) = P(B) P(A | B)[/latex].
This rule may also be written as: [latex]P(A|B) = \frac{P\left(A\text{ AND }B\right)}{P\left(B\right)},[/latex] that is, the probability of [latex]A[/latex] given [latex]B[/latex] equals the probability of both [latex]A[/latex] and [latex]B[/latex] divided by the probability of [latex]B[/latex].
If [latex]A[/latex] and [latex]B[/latex] are independent, then the probability of A does not depend on the probability of B and [latex]P(A | B ) = P(A)[/latex]. As a result, [latex]P(A \text{ AND }B) = P(A|B) P(B)[/latex] becomes [latex]P(A \text{ AND }B) = P(A) P(B)[/latex].
Example
A school has 200 seniors of whom 140 will be going to college next year. Forty will be going directly to work. The remainder are taking a gap year. Of the seniors going to college, fifty play sports. Of the seniors going directly to work, thirty play sports. Five of the seniors taking a gap year play sports.
- What is the probability that a senior is taking a gap year?
- Are "taking a gap year" and "playing sports" independent events?
- Are "going to college" and "taking a gap year" independent events?
Solution
- [latex]\frac{200−140−40}{200}= \frac{20}{200}=0.1[/latex]
- Let A= "taking a gap year" and B= "playing sports." Then [latex]P(A)=0.1[/latex] from step one, and [latex]P(B)= \frac{50+30+5}{200}=0.425[/latex].
Thus [latex]P(A) \cdot P(B)=0.1 \cdot 0.425=0.0425[/latex], while [latex]P(A \text{ AND } B)=\frac{5}{200}=0.025[/latex]. Since these are not the same number, the events are not independent. - Let A= "taking a gap year" and B= "going to college." Then as before, [latex]P(A)=0.1[/latex] and [latex]P(B)= \frac{140}{200}=0.7[/latex].
Then [latex]P(A) \cdot P(B)=0.1 \cdot 0.7=0.07[/latex], while [latex]P(A \text{ AND } B)=0[/latex]. Since these are not the same number, the events are not independent.
They are, however, mutually exclusive, which we look at next.
Your Turn!
Suppose you are going to roll a dice twice. Show that A = "Roll a 6 on the first roll" and B = "Roll a 4 on the second roll" are independent events using the Multiplication Rule.
Solution
Logically, we know these are independent because the outcome of the first roll does not influence the outcome of the second roll. To show this using the multiplication rule:
[latex]P(A)=\frac{1}{6}[/latex] and [latex]P(B)=\frac{1}{6}[/latex]
[latex]P(A \text{ AND } B)=\frac{1}{36}[/latex], because there are 36 ways to roll a dice twice but only one way to get a 6 first and then a 4.
[latex]P(A) \cdot P(B)=\frac{1}{6} \cdot \frac{1}{6}= \frac{1}{36}=P(A \text{ AND } B)[/latex], so the events are independent.
The Addition Rule
If [latex]A[/latex] and [latex]B[/latex] are defined on a sample space, then: [latex]P(A \text{ OR } B) = P(A) + P(B) - P(A \text{ AND } B)[/latex].
If [latex]A[/latex] and [latex]B[/latex] are mutually exclusive, then [latex]P(A \text{ AND } B) = 0[/latex]. Then [latex]P(A \text{ OR } B) = P(A) + P(B) - P(A \text{ AND } B)[/latex] becomes [latex]P(A \text{ OR } B) = P(A) + P(B)[/latex].
Example
Klaus is trying to choose where to go on vacation. His two choices are: A = New Zealand and B = Alaska. Klaus can only afford one vacation; he is leaning towards New Zealand so the probability that he chooses A is [latex]P(A) = 0.6[/latex] and the probability that he chooses B is [latex]P(B) = 0.35[/latex].
- [latex]P(A \text{ AND } B) = 0[/latex] because Klaus can only afford to take one vacation.
- Therefore, the probability that he chooses either New Zealand or Alaska is [latex]P(A \text{ OR } B) = P(A) + P(B) = 0.6 + 0.35 = 0.95[/latex]. Note that the probability that he does not choose to go anywhere on vacation must be 0.05.
Example
A student goes to the library. Let events B = the student checks out a book and M = the student checks out a movie. Suppose that [latex]P(B) = 0.40, P(M) = 0.30[/latex] and [latex]P(M|B) = 0.5[/latex].
- Find [latex]P(B \text{ AND } M)[/latex].
- Find [latex]P(B \text{ OR } M)[/latex].
Solution
- [latex]P(B \text{ AND } M)=P(M|B)P(B)=(0.5)(0.4)=0.20[/latex]
- [latex]P(B \text{ OR } M)=P(B)+P(M)−P(B \text{ AND } M) =0.40+0.30−0.20=0.50[/latex]
Your Turn!
Carlos plays college soccer. He makes a goal 65% of the time he shoots. Carlos is going to attempt two goals in a row in the next game. A = the event Carlos is successful on his first attempt. [latex]P(A) = 0.65[/latex]. B = the event Carlos is successful on his second attempt. [latex]P(B) = 0.65[/latex]. Carlos tends to shoot in streaks. The probability that he makes the second goal GIVEN that he made the first goal is 0.90.
a. What is the probability that he makes both goals?
Solution
The problem is asking you to find [latex]P(A \text{ AND } B) = P(B \text{ AND } A)[/latex]. Since [latex]P(B|A) = 0.90[/latex], [latex]P(B \text{ AND } A) = P(B|A) P(A) = (0.90)(0.65) = 0.585[/latex].
Carlos makes the first and second goals with probability 0.585.
b. Are A and B independent?
Solution
No, they are not, because:
[latex]P(B \text{ AND } A) = 0.585[/latex], and [latex]P(B) \cdot P(A) = (0.65)(0.65) = 0.423[/latex].
However, [latex]0.423 \neq 0.585[/latex].
So, [latex]P(B \text{ AND } A)[/latex] is not equal to [latex]P(B) \cdot P(A)[/latex].
c. What is the probability that Carlos makes either the first goal or the second goal?
Solution
The problem is asking you to find [latex]P(A \text{ OR } B)[/latex].
[latex]P(A \text{ OR } B) = P(A) + P(B) - P(A \text{ AND } B) = 0.65 + 0.65 - 0.585 = 0.715[/latex]
Carlos makes either the first goal or the second goal with probability 0.715.
d. Are A and B mutually exclusive?
Solution
No, they are not because [latex]P(A \text{ AND } B) = 0.585[/latex].
To be mutually exclusive, [latex]P(A \text{ AND } B)[/latex] must equal zero.
Your Turn!
A community swim team has 150 members. Seventy-five of the members are advanced swimmers. Forty-seven of the members are intermediate swimmers. The remainder are novice swimmers. Forty of the advanced swimmers practice four times a week. Thirty of the intermediate swimmers practice four times a week. Ten of the novice swimmers practice four times a week. Suppose one member of the swim team is chosen randomly.
- What is the probability that the member is a novice swimmer?
- What is the probability that the member practices four times a week?
- What is the probability that the member is an advanced swimmer and practices four times a week?
- What is the probability that a member is an advanced swimmer and an intermediate swimmer? Are being an advanced swimmer and an intermediate swimmer mutually exclusive? Why or why not?
- Are being a novice swimmer and practicing four times a week independent events? Why or why not?
Solution
- [latex]\frac{28}{150}= \frac{14}{75} \approx 0.187[/latex]
- [latex]\frac{80}{150}=\frac{8}{15} \approx 0.53[/latex]
- [latex]\frac{40}{150}= \frac{4}{15} \approx 0.27[/latex]
- [latex]P(\text{advanced AND intermediate}) = 0[/latex], because every swimmer has just one skill level. Since a swimmer cannot be advanced and intermediate at the same time, these are mutually exclusive events.
- [latex]P(\text{novice}) \cdot P(\text{practices four times per week}) = 0.0996[/latex]
[latex]P(\text{novice AND practices four times per week}) = 0.0667[/latex]
Since these are not equal, novice and practicing four times a week are not independent events.
Let us now look at some examples where we include the complement of events. As a reminder, the complement of an event [latex]A[/latex] is denoted [latex]A'[/latex], and [latex]P(A') = 1-P(A)[/latex].
Example
Studies show that about one woman in seven (approximately 14.3%) who live to be 90 will develop breast cancer. Suppose that of those women who develop breast cancer, a test is negative 2% of the time. Also suppose that in the general population of women, the test for breast cancer is negative about 85% of the time. Let B = woman develops breast cancer and let N = tests negative. Suppose one woman is selected at random.
- What is the probability that the woman develops breast cancer? What is the probability that the woman tests negative?
- Given that the woman has breast cancer, what is the probability that she tests negative?
- What is the probability that the woman has breast cancer and tests negative?
- What is the probability that the woman has breast cancer or tests negative?
- Are having breast cancer and testing negative mutually exclusive?
- Given that a woman develops breast cancer, what is the probability that she tests positive?
- What is the probability that a woman develops breast cancer and tests positive?
- What is the probability that a woman does not develop breast cancer?
- What is the probability that a woman tests positive for breast cancer?
Solution
- These probabilities are in the given information. [latex]P(B)=\frac{1}{7} \approx 0.143[/latex], and [latex]P(N)=0.85[/latex].
- Also in the provided information, [latex]P(N|B)=0.02[/latex].
- [latex]P(B \text{ AND } N)=P(B) \cdot P(N|B)=(0.143)(0.02)=0.0029[/latex]
- [latex]P(B \cup N)=P(B)+P(N)−P(B \cap N)=0.143+0.85−0.0029=0.9901[/latex]
- [latex]P(N)=0.85[/latex] while [latex]P(N|B)=0.02[/latex]. So No, these are not independent.
Alternatively, [latex]P(N) \cdot P(B)=(0.85)(0.143)=0.12155[/latex] which is not the same as [latex]0.0029[/latex] from Solution 2. So again, these are dependent events. - Since N is the event "tests negative," N' is the event "tests positive." [latex]P(N^{\prime} |B)=1−P(N|B)=1−0.02=0.98[/latex]
- [latex]P(B \text{ AND } N^{\prime})=P(N^{\prime}|B)P(B)=(0.98)(0.143)=0.1401[/latex]
- [latex]P(B^{\prime})=1−P(B)=1−0.143=0.857[/latex]
- [latex]P(N^{\prime})=1−P(N)=1−0.85=0.15[/latex]
Your Turn!
Returning to the example, a student goes to the library, where events B = the student checks out a book and M = the student checks out a movie. Suppose that P(B) = 0.40, P(M) = 0.30 and P(M|B) = 0.5.
- Find [latex]P(B^{\prime} )[/latex].
- Find [latex]P(M \text{ AND } B)[/latex].
- Find [latex]P(B | M)[/latex].
- Find [latex]P(M \text{ AND } B′)[/latex].
- Find [latex]P(M | B^{\prime} )[/latex].
Solution
- [latex]P(B^{\prime})=1−P(B)=0.60[/latex]
- [latex]P(M\cap B)=P(B) \cdot P(M|B)=(0.4)(0.5)=0.2[/latex]
- [latex]P(B|M)=\frac{P(B \cap M)}{P(M)}=\frac{0.20}{0.30}=\frac{2}{3} \approx 0.67[/latex]
- [latex]P(M \cap B^{\prime})=P(M) \cdot P(B^{\prime}|M)=P(M) \cdot (1−P(B|M))=(0.3) \left(1−\frac{2}{3} \right)=0.10[/latex]
- [latex]P(M|B^{\prime})= \frac{P(M \cap B ^{\prime})}{P(B^{\prime})}=\frac{0.10}{0.60}=\frac{1}{6}[/latex]
Section 3.3 Review
The multiplication rule and the addition rule are used for computing the probability of [latex]A[/latex] and [latex]B[/latex], as well as the probability of [latex]A[/latex] and [latex]B[/latex] for two given events [latex]A[/latex] and [latex]B[/latex] defined on the sample space. In sampling with replacement each member of a population is replaced after it is picked, so that member has the possibility of being chosen more than once, and the events are considered to be independent. In sampling without replacement, each member of a population may be chosen only once, and the events are considered to be not independent. The events [latex]A[/latex] and [latex]B[/latex] are mutually exclusive events when they do not have any outcomes in common.
Formula Review
The multiplication rule: [latex]P(A \text{ AND } B) = P(A | B)P(B)[/latex] or equivalently, [latex]P(A \cap B ) = P(A | B)P(B)[/latex]
The addition rule: [latex]P(A \text{ OR } B) = P(A) + P(B) - P(A \text{ AND } B)[/latex] or equivalently, [latex]P(A \cup B) = P(A) + P(B) - P(A \cap B)[/latex]
Section 3.3 Practice
Use the following information to answer the next ten exercises. Forty-eight percent of all Californians registered voters prefer life in prison without parole over the death penalty for a person convicted of first degree murder. Among Latino California registered voters, 55% prefer life in prison without parole over the death penalty for a person convicted of first degree murder. 37.6% of all Californians are Latino.
In this problem, let:
- C = Californians (registered voters) preferring life in prison without parole over the death penalty for a person convicted of first degree murder.
- L = Latino Californians
Suppose that one Californian is randomly selected.
1. Find [latex]P(C)[/latex].
2. Find [latex]P(L)[/latex].
Solution
0.376
3. Find [latex]P(C|L)[/latex].
4. In words, what is [latex]C|L[/latex]?
Solution
C|L means, given the person chosen is a Latino Californian, the person is a registered voter who prefers life in prison without parole for a person convicted of first degree murder.
5. Find [latex]P(L \text{ AND } C)[/latex].
6. In words, what is L AND C?
Solution
L AND C is the event that the person chosen is a Latino California registered voter who prefers life without parole over the death penalty for a person convicted of first degree murder.
7. Are L and C independent events? Show why or why not.
8. Find [latex]P(L \text{ OR } C)[/latex].
Solution
0.6492
9. In words, what is L OR C?
10. Are L and C mutually exclusive events? Show why or why not.
Solution
No, because [latex]P(L \text{ AND } C)[/latex] does not equal 0.
On February 28, 2013, a Field Poll Survey reported that 61% of California registered voters approved of allowing two people of the same gender to marry and have regular marriage laws apply to them. Among 18 to 39 year olds (California registered voters), the approval rating was 78%. Six in ten California registered voters said that the upcoming Supreme Court’s ruling about the constitutionality of California’s Proposition 8 was either very or somewhat important to them. Out of those CA registered voters who support same-sex marriage, 75% say the ruling is important to them.
In this problem, let:
- C = California registered voters who support same-sex marriage.
- B = California registered voters who say the Supreme Court’s ruling about the constitutionality of California’s Proposition 8 is very or somewhat important to them
- A = California registered voters who are 18 to 39 years old.
- Find [latex]P(C)[/latex].
- Find [latex]P(B)[/latex].
- Find [latex]P(C|A)[/latex].
- Find [latex]P(B|C)[/latex].
- In words, what is C|A?
- In words, what is B|C?
- Find [latex]P(C \text{ AND } B)[/latex].
- In words, what is C AND B?
- Find [latex]P(C \text{ OR } B)[/latex].
- Are C and B mutually exclusive events? Show why or why not.
After Rob Ford, the mayor of Toronto, announced his plans to cut budget costs in late 2011, the Forum Research polled 1,046 people to measure the mayor’s popularity. Everyone polled expressed either approval or disapproval. These are the results their poll produced:
- In early 2011, 60 percent of the population approved of Mayor Ford’s actions in office.
- In mid-2011, 57 percent of the population approved of his actions.
- In late 2011, the percentage of popular approval was measured at 42 percent.
- What is the sample size for this study?
- What proportion in the poll disapproved of Mayor Ford, according to the results from late 2011?
- How many people polled responded that they approved of Mayor Ford in late 2011?
- What is the probability that a person supported Mayor Ford, based on the data collected in mid-2011?
- What is the probability that a person supported Mayor Ford, based on the data collected in early 2011?
Solution
- The Forum Research surveyed 1,046 Torontonians.
- 58%
- 42% of 1,046 = 439 (rounding to the nearest integer)
- 0.57
- 0.60.
Use the following information to answer the following exercises. The casino game, roulette, allows the gambler to bet on the probability of a ball, which spins in the roulette wheel, landing on a particular color, number, or range of numbers. The table used to place bets contains 38 numbers, and each number is assigned to a color and a range.
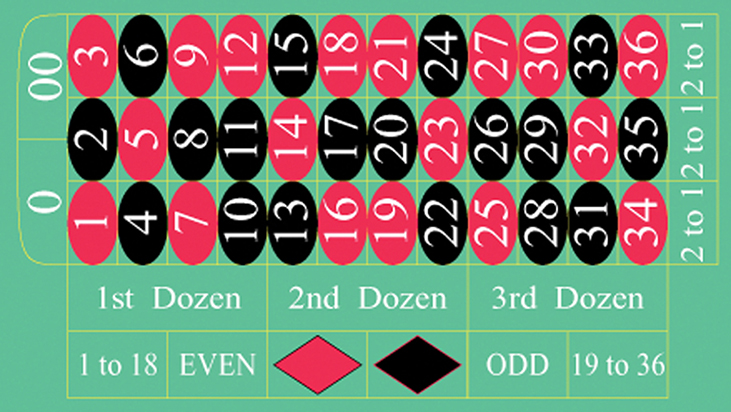
- Find the following probabilities.
- List the sample space of the 38 possible outcomes in roulette.
- You bet on red. Find P(red).
- You bet on -1st 12- (1st Dozen). Find P(-1st 12-).
- You bet on an even number. Find P(even number). Is getting an odd number the complement of getting an even number? Why?
- Find two mutually exclusive events.
- Are the events Even and 1st Dozen independent?
- Compute the probability of winning the following types of bets:
- Betting on two lines that touch each other on the table as in 1-2-3-4-5-6
- Betting on three numbers in a line, as in 1-2-3
- Betting on one number
- Betting on four numbers that touch each other to form a square, as in 10-11-13-14
- Betting on two numbers that touch each other on the table, as in 10-11 or 10-13
- Betting on 0-00-1-2-3
- Betting on 0-1-2; or 0-00-2; or 00-2-3
- Compute the probability of winning the following types of bets:
- Betting on a color
- Betting on one of the dozen groups
- Betting on the range of numbers from 1 to 18
- Betting on the range of numbers 19–36
- Betting on one of the columns
- Betting on an even or odd number (excluding zero)
Solution to number 4
- P(Betting on two line that touch each other on the table) = [latex]\frac{6}{38}[/latex]
- P(Betting on three numbers in a line) = [latex]\frac{3}{38}[/latex]
- P(Betting on one number) = [latex]\frac{1}{38}[/latex]
- P(Betting on four number that touch each other to form a square) = [latex]\frac{4}{38}[/latex]
- P(Betting on two number that touch each other on the table) = [latex]\frac{2}{38}[/latex]
- P(Betting on 0-00-1-2-3) = [latex]\frac{5}{38}[/latex]
- P(Betting on 0-1-2; or 0-00-2; or 00-2-3) = [latex]\frac{3}{38}[/latex]
Suppose that you have eight cards. Five are green and three are yellow. The five green cards are numbered 1, 2, 3, 4, and 5. The three yellow cards are numbered 1, 2, and 3. The cards are well shuffled. You randomly draw one card.
- G = card drawn is green
- E = card drawn is even-numbered
- List the sample space.
- [latex]P(G) = \underline{\hspace{2cm}}[/latex]
- [latex]P(G|E) = \underline{\hspace{2cm}}[/latex]
- [latex]P(G \text{ AND } E) = \underline{\hspace{2cm}}[/latex]
- [latex]P(G \text{ OR } E) = \underline{\hspace{2cm}}[/latex]
- Are G and E mutually exclusive? Justify your answer numerically.
Solution
- {G1, G2, G3, G4, G5, Y1, Y2, Y3}
- [latex]\frac{5}{8}\text{}[/latex]
- [latex]\frac{2}{3}\text{}[/latex]
- [latex]\frac{2}{8}\text{}[/latex]
- [latex]\frac{6}{8}\text{}[/latex]
- No, because [latex]P(G \text{ AND } E)[/latex] does not equal 0.
Roll two fair dice. Each die has six faces.
- List the sample space.
- Let A be the event that either a three or four is rolled first, followed by an even number. Find [latex]P(A)[/latex].
- Let B be the event that the sum of the two rolls is at most seven. Find [latex]P(B)[/latex].
- In words, explain what “[latex]P(A|B)[/latex]” represents. Find [latex]P(A|B)[/latex].
- Are A and B mutually exclusive events? Explain your answer in one to three complete sentences, including numerical justification.
- Are A and B independent events? Explain your answer in one to three complete sentences, including numerical justification.
A special deck of cards has ten cards. Four are green, three are blue, and three are red. When a card is picked, its color is recorded. An experiment consists of first picking a card and then tossing a coin.
- List the sample space.
- Let A be the event that a blue card is picked first, followed by landing a head on the coin toss. Find P(A).
- Let B be the event that a red or green is picked, followed by landing a head on the coin toss. Are the events A and B mutually exclusive? Explain your answer in one to three complete sentences, including numerical justification.
- Let C be the event that a red or blue is picked, followed by landing a head on the coin toss. Are the events A and C mutually exclusive? Explain your answer in one to three complete sentences, including numerical justification.
Solution
Note: The coin toss is independent of the card picked first.
- {(G,H) (G,T) (B,H) (B,T) (R,H) (R,T)}
- [latex]P(A) = P(\text{blue})P(\text{head}) = \left(\frac{3}{10}\right) \left(\frac{1}{2}\right) = \frac{3}{20}[/latex]
- Yes, A and B are mutually exclusive because they cannot happen at the same time; you cannot pick a card that is both blue and also (red or green). [latex]P(A \text{ AND } B) = 0[/latex]
- No, A and C are not mutually exclusive because they can occur at the same time. In fact, C includes all of the outcomes of A; if the card chosen is blue it is also (red or blue). [latex]P(A \text{ AND } C) = P(A) = \frac{3}{20}[/latex]
An experiment consists of first rolling a die and then tossing a coin.
1. List the sample space.
2. Let A be the event that either a three or a four is rolled first, followed by landing a head on the coin toss. Find [latex]P(A)[/latex].
3. Let B be the event that the first and second tosses land on heads. Are the events A and B mutually exclusive? Explain your answer in one to three complete sentences, including numerical justification.
An experiment consists of tossing a nickel, a dime, and a quarter. Of interest is the side the coin lands on.
- List the sample space.
- Let A be the event that there are at least two tails. Find [latex]P(A)[/latex].
- Let B be the event that the first and second tosses land on heads. Are the events A and B mutually exclusive? Explain your answer in one to three complete sentences, including justification.
Solution
- S = {(HHH), (HHT), (HTH), (HTT), (THH), (THT), (TTH), (TTT)}
- [latex]\frac{4}{8}[/latex]
- Yes, because if A has occurred, it is impossible to obtain two tails. In other words, [latex]P(A \text{ AND } B) = 0[/latex].
Consider the following scenario:
- Let [latex]P(C) = 0.4[/latex].
- Let [latex]P(D) = 0.5[/latex].
- Let [latex]P(C|D) = 0.6[/latex].
- Find [latex]P(C \text{ AND } D)[/latex].
- Are C and D mutually exclusive? Why or why not?
- Are C and D independent events? Why or why not?
- Find [latex]P(C \text{ OR } D)[/latex].
- Find [latex]P(D|C)[/latex].
Y and Z are independent events.
- Rewrite the basic Addition Rule [latex]P(Y \text{ OR } Z) = P(Y) + P(Z) - P(Y \text{ AND } Z)[/latex] using the information that Y and Z are independent events.
- Use the rewritten rule to find [latex]P(Z)[/latex] if [latex]P(Y \text{ OR } Z) = 0.71[/latex] and [latex]P(Y) = 0.42[/latex].
Solution
- If Y and Z are independent, then [latex]P(Y \text{ AND } Z) = P(Y)P(Z)[/latex], so [latex]P(Y \text{ OR } Z) = P(Y) + P(Z) - P(Y)P(Z)[/latex].
- 0.5
G and H are mutually exclusive events. [latex]P(G) = 0.5 P(H) = 0.3[/latex]
1. Explain why the following statement MUST be false: [latex]P(H|G) = 0.4[/latex].
2. Find [latex]P(H \text{ OR } G)[/latex].
3. Are G and H independent or dependent events? Explain in a complete sentence.
Approximately 281,000,000 people over age five live in the United States. Of these people, 55,000,000 speak a language other than English at home. Of those who speak another language at home, 62.3% speak Spanish.
Let: E = speaks English at home; E′ = speaks another language at home; S = speaks Spanish;
Finish each probability statement by matching the correct answer.
| Probability Statements | Answers |
|---|---|
| a. P(E′) = | i. 0.8043 |
| b. P(E) = | ii. 0.623 |
| c. P(S and E′) = | iii. 0.1957 |
| d. P(S|E′) = | iv. 0.1219 |
In 1994, the U.S. government held a lottery to issue 55,000 Green Cards (permits for non-citizens to work legally in the U.S.). Renate Deutsch, from Germany, was one of approximately 6.5 million people who entered this lottery. Let G = won green card.
- What was Renate’s chance of winning a Green Card? Write your answer as a probability statement.
- In the summer of 1994, Renate received a letter stating she was one of 110,000 finalists chosen. Once the finalists were chosen, assuming that each finalist had an equal chance to win, what was Renate’s chance of winning a Green Card? Write your answer as a conditional probability statement. Let F = was a finalist.
- Are G and F independent or dependent events? Justify your answer numerically and also explain why.
- Are G and F mutually exclusive events? Justify your answer numerically and explain why.
Three professors at George Washington University did an experiment to determine if economists are more selfish than other people. They dropped 64 stamped, addressed envelopes with $10 cash in different classrooms on the George Washington campus. 44% were returned overall. From the economics classes 56% of the envelopes were returned. From the business, psychology, and history classes 31% were returned.
Let: R = money returned; E = economics classes; O = other classes
- Write a probability statement for the overall percent of money returned.
- Write a probability statement for the percent of money returned out of the economics classes.
- Write a probability statement for the percent of money returned out of the other classes.
- Is money being returned independent of the class? Justify your answer numerically and explain it.
- Based upon this study, do you think that economists are more selfish than other people? Explain why or why not. Include numbers to justify your answer.
Solution
- [latex]P(R) = 0.44[/latex]
- [latex]P(R|E) = 0.56[/latex]
- [latex]P(R|O) = 0.31[/latex]
- No, whether the money is returned is not independent of which class the money was placed in. There are several ways to justify this mathematically, but one is that the money placed in economics classes is not returned at the same overall rate; [latex]P(R|E) \neq P(R)[/latex].
- No, this study definitely does not support that notion; in fact, it suggests the opposite. The money placed in the economics classrooms was returned at a higher rate than the money place in all classes collectively; [latex]P(R|E) > P(R)[/latex].
The following table of data obtained from www.baseball-almanac.com shows hit information for four players. Suppose that one hit from the table is randomly selected.
| Name | Single | Double | Triple | Home Run | Total Hits |
|---|---|---|---|---|---|
| Babe Ruth | 1,517 | 506 | 136 | 714 | 2,873 |
| Jackie Robinson | 1,054 | 273 | 54 | 137 | 1,518 |
| Ty Cobb | 3,603 | 174 | 295 | 114 | 4,189 |
| Hank Aaron | 2,294 | 624 | 98 | 755 | 3,771 |
| Total | 8,471 | 1,577 | 583 | 1,720 | 12,351 |
Are "the hit being made by Hank Aaron" and "the hit being a double" independent events? Choose the best answer.
a. Yes, because [latex]P(\text{hit by Hank Aaron|hit is a double}) = P(\text{hit by Hank Aaron})[/latex]
b. No, because [latex]P(\text{hit by Hank Aaron|hit is a double}) \neq P(\text{hit is a double})[/latex]
c. No, because [latex]P(\text{hit is by Hank Aaron|hit is a double}) \neq P(\text{hit by Hank Aaron})[/latex]
d. Yes, because [latex]P(\text{hit is by Hank Aaron|hit is a double}) = P(\text{hit is a double})[/latex]
United Blood Services is a blood bank that serves more than 500 hospitals in 18 states. According to their website, a person with type O blood and a negative Rh factor (Rh-) can donate blood to any person with any blood type. Their data show that 43% of people have type O blood and 15% of people have Rh- factor; 52% of people have type O or Rh- factor.
- Find the probability that a person has both type O blood and the Rh- factor.
- Find the probability that a person does NOT have both type O blood and the Rh- factor.
Solution
-
[latex]P(\text{type O OR Rh-}) = P(\text{type O}) + P(\text{Rh-}) - P(\text{type O AND Rh-})[/latex]
0.52 = 0.43 + 0.15 - P(type O AND Rh-); solve to find P(type O AND Rh-) = 0.06
6% of people have type O, Rh- blood
-
[latex]P(\text{NOT(type O AND Rh-)}) = 1 - P(\text{type O AND Rh-}) = 1 - 0.06 = 0.94[/latex]
94% of people do not have type O, Rh- blood
At a college, 72% of courses have final exams and 46% of courses require research papers. Suppose that 32% of courses have a research paper and a final exam. Let F be the event that a course has a final exam. Let R be the event that a course requires a research paper.
- Find the probability that a course has a final exam or a research project.
- Find the probability that a course has NEITHER of these two requirements.
In a box of assorted cookies, 36% contain chocolate and 12% contain nuts. Of those, 8% contain both chocolate and nuts. Sean is allergic to both chocolate and nuts.
- Find the probability that a cookie contains chocolate or nuts (he can't eat it).
- Find the probability that a cookie does not contain chocolate or nuts (he can eat it).
Solution
Let C = be the event that the cookie contains chocolate. Let N = the event that the cookie contains nuts.
- [latex]P(C \text{ OR } N) = P(C) + P(N) - P(C \text{ AND } N) = 0.36 + 0.12 - 0.08 = 0.40[/latex]
- [latex]P(\text{NEITHER chocolate NOR nuts}) = 1 - P(C \text{ OR } N) = 1 - 0.40 = 0.60[/latex]
A college finds that 10% of students have taken a distance learning class and that 40% of students are part time students. Of the part time students, 20% have taken a distance learning class. Let D = event that a student takes a distance learning class and E = event that a student is a part time student
- Find [latex]P(D \text{ AND } E)[/latex].
- Find [latex]P(E|D)[/latex].
- Find [latex]P(D \text{ OR } E)[/latex].
- Using an appropriate test, show whether D and E are independent.
- Using an appropriate test, show whether D and E are mutually exclusive.
References
DiCamillo, Mark, Mervin Field. “The File Poll.” Field Research Corporation. Available online at http://www.field.com/fieldpollonline/subscribers/Rls2443.pdf (accessed May 2, 2013).
Rider, David, “Ford support plummeting, poll suggests,” The Star, September 14, 2011. Available online at http://www.thestar.com/news/gta/2011/09/14/ford_support_plummeting_poll_suggests.html (accessed May 2, 2013).
“Mayor’s Approval Down.” News Release by Forum Research Inc. Available online at http://www.forumresearch.com/forms/News Archives/News Releases/74209_TO_Issues_-_Mayoral_Approval_%28Forum_Research%29%2820130320%29.pdf (accessed May 2, 2013).
“Roulette.” Wikipedia. Available online at http://en.wikipedia.org/wiki/Roulette (accessed May 2, 2013).
Shin, Hyon B., Robert A. Kominski. “Language Use in the United States: 2007.” United States Census Bureau. Available online at http://www.census.gov/hhes/socdemo/language/data/acs/ACS-12.pdf (accessed May 2, 2013).
Data from the Baseball-Almanac, 2013. Available online at www.baseball-almanac.com (accessed May 2, 2013).
Data from U.S. Census Bureau.
Data from the Wall Street Journal.
Data from The Roper Center: Public Opinion Archives at the University of Connecticut. Available online at http://www.ropercenter.uconn.edu/ (accessed May 2, 2013).
Data from Field Research Corporation. Available online at www.field.com/fieldpollonline (accessed May 2,2 013).
Two events that cannot happen at the same; they share no common outcomes
The occurrence of one event has no effect on the probability of the occurrence of another event
The occurrence of one event has no effect on the probability of the occurrence of another event. Events A and B are independent if one of the following is true:
• P(A|B) = P(A)
• P(B|A) = P(B)
• P(A AND B) = P(A)P(B)
Two events are mutually exclusive if the probability that they both happen at the same time is zero. If events A and B are mutually exclusive, then P(A AND B) = 0.

