"

Chapter 4: Discrete Random Variables

4.5 Hypergeometric Distribution

Learning Objectives

By the end of this section, you should be able to:

  • Identify the components of a hypergeometric experiment
  • Use the formulas for a hypergeometric random variable to compute the mean

There are five characteristics of a hypergeometric experiment.

  1. You take samples from two groups.
  2. You are concerned with a group of interest, called the first group.
  3. You sample without replacement from the combined groups. For example, you want to choose a softball team from a combined group of 11 men and 13 women. The team consists of ten players.
  4. Each pick is not independent, since sampling is without replacement. In the softball example, the probability of picking a woman first is [latex]\frac{13}{24}[/latex]. The probability of picking a man second is [latex]\frac{11}{23}[/latex] if a woman was picked first. It is [latex]\frac{10}{23}[/latex] if a man was picked first. The probability of the second pick depends on what happened in the first pick.
  5. You are not dealing with Bernoulli Trials.

The outcomes of a hypergeometric experiment fit a hypergeometric probability distribution. The random variable [latex]X =[/latex]the number of items from the group of interest.

Example

A candy dish contains 100 jelly beans and 80 gumdrops. Fifty candies are picked at random. What is the probability that 35 of the 50 are gumdrops?

This experiment is hypergeometric: the two groups are jelly beans and gumdrops. Since the probability question asks for the probability of picking gumdrops, the group of interest (first group) is gumdrops and size 80. The size of the second group, jelly beans, is 100. The size of the sample is 50 (jelly beans or gumdrops).

Let [latex]X =[/latex] the number of gumdrops in the sample of 50. [latex]X[/latex] takes on the values [latex]x = 0, 1, 2, ..., 50[/latex]. What is the probability statement written mathematically?

Solution

[latex]P(x = 35)[/latex]

Your Turn!

A bag contains letter tiles. Forty-four of the tiles are vowels, and 56 are consonants. Seven tiles are picked at random. You want to know the probability that four of the seven tiles are vowels. What is the group of interest, the size of the group of interest, and the size of the sample?

Solution

The group of interest is the vowel letter tiles. The size of the group of interest is 44. The size of the sample is seven.

Your Turn!

You are president of an on-campus special events organization. You need a committee of seven students to plan a special birthday party for the president of the college. Your organization consists of 18 women and 15 men. If the members of the committee are randomly selected, what is the probability that your committee has more than four men?

a. Are you choosing with or without replacement?

Solution

without

 

b. What is the group of interest?

Solution

the men

 

c. How many are in the group of interest?

Solution

15 men

 

d. How many are in the other group?

Solution

18 women

 

e. Let [latex]X = \underline{\hspace{2cm}}[/latex] on the committee. What values does [latex]X[/latex] take on?

Solution

Let [latex]X =[/latex]the number of men on the committee. [latex]x = 0, 1, 2, …, 7[/latex].

 

f. The probability question is [latex]P( \underline{\hspace{2cm}} )[/latex].

Solution

[latex]P(x > 4)[/latex]

Notation and Mean for the Hypergeometric

The notation for the Geometric Probability Distribution function is [latex]H[/latex], and we denote “[latex]X[/latex] is a random variable with a hypergeometric probability distribution as [latex]X \sim{H(r, b, n)}[/latex].

The parameters are [latex]r[/latex], [latex]b[/latex], and [latex]n[/latex]; [latex]r =[/latex] the size of the group of interest (first group), [latex]b =[/latex] the size of the second group, [latex]n =[/latex]the size of the chosen sample. Most of the formulas for the Hypergeometric distribution are beyond the scope of this book; the exception is the mean.

[latex]\mu =\frac{nr}{r+b}[/latex]

Note

Currently, the TI-83/84 calculators do not have a built-in hypergeometric distribution button. You can calculate probabilities in Excel using HYPGEO.DIST(x, n, r, r+b, True/False), where False computes [latex]P(X=x)[/latex], and True computes [latex]P(X \leq x)[/latex].

Your Turn!

A school site committee is to be chosen randomly from five men and six women. (1) If the committee consists of four members chosen randomly, what is the probability that two of them are women? (2) How many women do you expect to be on the committee?

Let [latex]X =[/latex] the number of women on the committee of four. The women are the group of interest (first group). The random variable [latex]X[/latex] takes on the values 0, 1, 2, 3, 4, where [latex]r = 6[/latex], [latex]b = 5[/latex], and [latex]n = 4[/latex], and [latex]X \sim H(6, 5, 4)[/latex].

The graph of [latex]X \sim H(6, 5, 4)[/latex] is below.

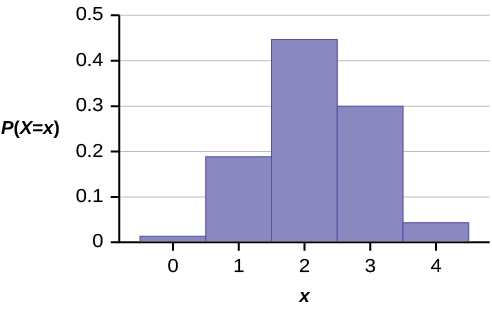
This graph shows a hypergeometric probability distribution. It has five bars that are slightly normally distributed. The x-axis shows values from 0 to 4 in increments of 1, representing the number of men on the four-person committee. The y-axis ranges from 0 to 0.5 in increments of 0.1.

The y-axis contains the probability of [latex]X[/latex], where [latex]X =[/latex] the number of men on the committee.

Solution

(1) Using Excel’s HypGeom.Dist, [latex]P(X = 2) = \text{HYPGEOM.DIST}(2,4,6,11, \text{FALSE}) \approx 0.4545[/latex]. The probability that there are exactly two women on the committee is about 0.45.

(2) The formula for the mean is [latex]\mu =\frac{nr}{r+b}=\frac{\left(4\right)\left(6\right)}{6+5}=2.18[/latex]. You would expect [latex]\mu= 2.18[/latex] (about two) women on the committee.

Your Turn!

An intramural basketball team is to be chosen randomly from 15 upperclassmen and 12 underclassmen. The team has ten slots. You want to know the probability that eight of the players will be upperclassmen. What is the group of interest and the sample? Find the probability using a computer.

Solution

The group of interest are the upperclassmen, and the sample is 10. We have [latex]P(X=8)=\text{HYPGEOM.DIST}(8,10,15,27,\text{FALSE}) \approx 0.05[/latex].

Section 4.5 Review

A hypergeometric experiment is a statistical experiment with the following properties:

  1. You take samples from two groups.
  2. You are concerned with a group of interest, called the first group.
  3. You sample without replacement from the combined groups.
  4. Each pick is not independent, since sampling is without replacement.
  5. You are not dealing with Bernoulli Trials.

The outcomes of a hypergeometric experiment fit a hypergeometric probability distribution. The random variable [latex]X= \text{the number of items from the group of interest}[/latex]. The distribution of[latex]X[/latex] is denoted [latex]X \sim H(r,b,n)[/latex], where [latex]r= \text{the size of the group of interest (first group)}[/latex], [latex]b= \text{the size of the second group}[/latex], and [latex]n = \text{the size of the chosen sample}[/latex]. It follows that [latex]n \leq r+b[/latex]. The mean of [latex]X[/latex]  is [latex]\mu = \frac{nr}{r+ b}[/latex] and the standard deviation is [latex]\sigma = \sqrt{\frac{rbn(r+b− n)}{(r + b)^{2}(r + b-1)}}[/latex].

Formula Review

 [latex]X \sim H(r,b,n)[/latex] means that the discrete random variable [latex]X[/latex]  has a hypergeometric probability distribution with [latex]r= \text{the size of the group of interest (first group)}[/latex], [latex]b= \text{the size of the second group}[/latex], and [latex]n = \text{the size of the chosen sample}[/latex].

[latex]X= \text{the number of items from the group of interest that are in the chosen sample}[/latex]

[latex]X[/latex] may take on the values [latex]x = 0, 1, 2, \ldots[/latex] up to the size of the group of interest. (The minimum value for [latex]X[/latex] may be larger than zero in some instances.)

[latex]n \leq r+b[/latex]

[latex]\mu = \frac{nr}{r+ b}[/latex]

[latex]\sigma = \sqrt{\frac{rbn(r+b− n)}{(r + b)^{2}(r + b-1)}}[/latex]

Section 4.5 Practice

Use the following information to answer the next five exercises: Suppose that a group of statistics students is divided into two groups: business majors and non-business majors. There are 16 business majors in the group and seven non-business majors in the group. A random sample of nine students is taken. We are interested in the number of business majors in the sample.

In words, define the random variable [latex]X[/latex].

Solution

1. [latex]X =[/latex]the number of business majors in the sample.

 

2. [latex]X \sim \underline{\hspace{2cm}} ( \underline{\hspace{2cm}} , \underline{\hspace{2cm}} )[/latex]

 

3. What values does [latex]X[/latex] take on?

Solution

[latex]2, 3, 4, 5, 6, 7, 8, 9[/latex]

 

4. Find the standard deviation.

 

5. On average ([latex]\mu[/latex]), how many would you expect to be business majors?

Solution

6.26

A group of Martial Arts students is planning on participating in an upcoming demonstration. Six are students of Tae Kwon Do; seven are students of Shotokan Karate. Suppose that eight students are randomly picked to be in the first demonstration. We are interested in the number of Shotokan Karate students in that first demonstration.

  1. In words, define the random variable [latex]X[/latex].
  2. List the values that [latex]X[/latex] may take on.
  3. Give the distribution of [latex]X[/latex]. [latex]X \sim \underline{\hspace{2cm}} ( \underline{\hspace{2cm}} , \underline{\hspace{2cm}} )[/latex]
  4. How many Shotokan Karate students do we expect to be in that first demonstration?
Solution
  1. [latex]X =[/latex] the number of Shotokan Karate students in the first demonstration
  2. [latex]1, 2, 3, 4, 5, 6, 7[/latex]
  3. [latex]X \sim H(7, 6, 8)[/latex]
  4. 4.31

In one of its Spring catalogs, L.L. Bean® advertised footwear on 29 of its 192 catalog pages. Suppose we randomly survey 20 pages. We are interested in the number of pages that advertise footwear. Each page may be picked at most once.

  1. In words, define the random variable [latex]X[/latex].
  2. List the values that [latex]X[/latex] may take on.
  3. Give the distribution of [latex]X[/latex]. [latex]X \sim \underline{\hspace{2cm}} ( \underline{\hspace{2cm}} , \underline{\hspace{2cm}} )[/latex]
  4. How many pages do you expect to advertise footwear on them?
  5. Calculate the standard deviation.
Solution
  1. [latex]X =[/latex] the number of pages that advertise footwear
  2. [latex]0, 1, 2, 3, ..., 20[/latex]
  3. [latex]X \sim H(29, 163, 20); r = 29, b = 163, n = 20[/latex]
  4. 3.03
  5. 1.5197

Suppose that a technology task force is being formed to study technology awareness among instructors. Assume that ten people will be randomly chosen to be on the committee from a group of 28 volunteers, 20 who are technically proficient and eight who are not. We are interested in the number on the committee who are not technically proficient.

  1. In words, define the random variable [latex]X[/latex].
  2. List the values that [latex]X[/latex] may take on.
  3. Give the distribution of [latex]X[/latex]. [latex]X \sim \underline{\hspace{2cm}} ( \underline{\hspace{2cm}} , \underline{\hspace{2cm}} )[/latex]
  4. How many instructors do you expect on the committee who are not technically proficient?
  5. Find the probability that at least five on the committee are not technically proficient.
  6. Find the probability that at most three on the committee are not technically proficient.
Solution
  1. [latex]X =[/latex] the number of people on the committee who are not technically proficient
  2. [latex]0, 1, 2, 3, 4, 5, 6, 7, 8[/latex]
  3. [latex]X \sim B(10, 8, 28)[/latex]
  4. 2.8571
  5. 0.0772
  6. 0.7160

Suppose that nine Massachusetts athletes are scheduled to appear at a charity benefit. The nine are randomly chosen from eight volunteers from the Boston Celtics and four volunteers from the New England Patriots. We are interested in the number of Patriots picked.

  1. In words, define the random variable [latex]X[/latex].
  2. List the values that [latex]X[/latex] may take on.
  3. Give the distribution of [latex]X[/latex]. [latex]X \sim \underline{\hspace{2cm}} ( \underline{\hspace{2cm}} , \underline{\hspace{2cm}} )[/latex]
  4. Are you choosing the nine athletes with or without replacement?
Solution
  1. [latex]X =[/latex] the number of Patriots picked
  2. [latex]0, 1, 2, 3, 4[/latex]
  3. [latex]X \sim H(4, 8, 9)[/latex]
  4. Without replacement

A bridge hand is defined as 13 cards selected at random and without replacement from a deck of 52 cards. In a standard deck of cards, there are 13 cards from each suit: hearts, spades, clubs, and diamonds. What is the probability of being dealt a hand that does not contain a heart?

  1. What is the group of interest?
  2. How many are in the group of interest?
  3. How many are in the other group?
  4. Let [latex]X = \underline{\hspace{2cm}}[/latex]. What values does X take on?
  5. The probability question is [latex]P( \underline{\hspace{2cm}} )[/latex].
  6. Find the probability in question.
  7. Find the (i) mean and (ii) standard deviation of [latex]X[/latex].
definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Introductory Statistics Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book