"

Chapter 5: Continuous Random Variables

5.1 Continuous Probability Functions

Learning Objectives

By the end of this section, students will be able to:

  • describe the properties of continuous probability distributions.

Properties of Continuous Probability Distributions

The graph of a continuous probability distribution is a curve. Probability is represented by area under the curve.

The curve is called the probability density function (abbreviated as pdf). We use the symbol [latex]f(x)[/latex] to represent the curve. [latex]f(x)[/latex] is the function that corresponds to the graph; we use the density function [latex]f(x)[/latex] to draw the graph of the probability distribution.

Area under the curve is given by a different function called the cumulative distribution function (abbreviated as cdf). The cumulative distribution function is used to evaluate probability as area.

  • The outcomes are measured, not counted.
  • The entire area under the curve and above the x-axis is equal to one.
  • Probability is found for intervals of x values rather than for individual [latex]x[/latex] values.
  • [latex]P(c \lt x \lt d)[/latex] is the probability that the random variable [latex]X[/latex] is in the interval between the values [latex]c[/latex] and [latex]d[/latex]. [latex]P(c \lt x \lt d)[/latex] is the area under the curve, above the x-axis, to the right of [latex]c[/latex] and the left of [latex]d[/latex].
  • [latex]P(x = c) = 0[/latex] The probability that x takes on any single individual value is zero. The area below the curve, above the x-axis, and between [latex]x = c[/latex] and [latex]x = c[/latex] has no width, and therefore no area (area = 0). Since the probability is equal to the area, the probability is also zero.
  • [latex]P(c \lt x \lt d)[/latex] is the same as [latex]P(c \le x \le d)[/latex] because probability is equal to area.

We will find the area that represents probability by using geometry, formulas, technology, or probability tables. In general, calculus is needed to find the area under the curve for many probability density functions. When we use formulas to find the area in this textbook, the formulas were found by using the techniques of integral calculus. However, because most students taking this course have not studied calculus, we will not be using calculus in this textbook.

There are many continuous probability distributions. When using a continuous probability distribution to model probability, the distribution used is selected to model and fit the particular situation in the best way.

In this chapter and the next, we will study the uniform distribution, the exponential distribution, and the normal distribution. The following graphs illustrate these distributions.

The graph shows a Uniform Distribution with the area between [latex]x = 3[/latex] and [latex]x = 6[/latex] shaded to represent the probability that the value of the random variable X is in the interval between three and six.

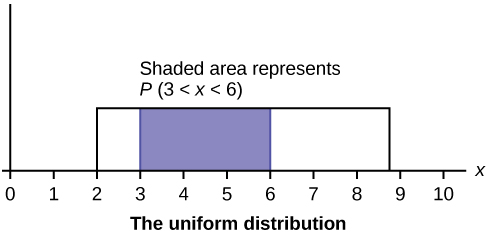
This graph shows a uniform distribution. The horizontal axis ranges from 0 to 10. The distribution is modeled by a rectangle extending from x = 2 to x = 8.8. A region from x = 3 to x = 6 is shaded inside the rectangle. The shaded area represents P(3 x < 6).

The graph shows an Exponential Distribution with the area between [latex]x = 2[/latex] and [latex]x = 4[/latex] shaded to represent the probability that the value of the random variable [latex]X[/latex] is in the interval between two and four.

The graph shows the Standard Normal Distribution with the area between [latex]x = 1[/latex] and [latex]x = 2[/latex] shaded to represent the probability that the value of the random variable [latex]X[/latex] is in the interval between one and two.

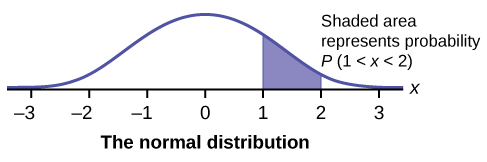
This graph shows an exponential distribution. The graph slopes downward. It begins at a point on the y-axis and approaches the x-axis at the right edge of the graph. The region under the graph from x = 2 to x = 4 is shaded to represent P(2 < x < 4).

Continuous Probability Functions

We begin by defining a continuous probability density function. We use the function notation [latex]f(x)[/latex]. Intermediate algebra may have been your first formal introduction to functions. In the study of probability, the functions we study are special. We define the function [latex]f(x)[/latex] so that the area between it and the x-axis is equal to a probability. Since the maximum probability is one, the maximum area is also one. For continuous probability distributions, PROBABILITY = AREA.

Example

Consider the function [latex]f(x) = \frac{1}{20}[/latex] for [latex]0 \le x \le 20[/latex]. [latex]x =[/latex] a real number. The graph of [latex]f(x) = \frac{1}{20}[/latex] is a horizontal line. However, since [latex]0 \le x \le 20[/latex], [latex]f(x)[/latex] is restricted to the portion between [latex]x = 0[/latex] and [latex]x = 20[/latex], inclusive.

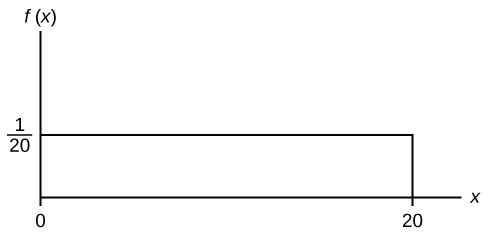
This shows the graph of the function f(x) = 1/20. A horizontal line ranges from the point (0, 1/20) to the point (20, 1/20). A vertical line extends from the x-axis to the end of the line at point (20, 1/20) creating a rectangle.

[latex]f(x)= \frac{1}{20}[/latex]for [latex]0 \le x \le 20[/latex].

The graph of [latex]f(x) = \frac{1}{20}[/latex] is a horizontal line segment when [latex]0 \le x \le 20[/latex].

The area between [latex]f(x) = \frac{1}{20}[/latex] where [latex]0 \le x \le 20[/latex] and the x-axis is the area of a rectangle with [latex]\text{base} = 20[/latex] and [latex]\text{height} = \frac{1}{20}[/latex].

[latex]\text{AREA}=20\left(\frac{1}{20}\right)=1[/latex]

Suppose we want to find the area between [latex]f(x) = \frac{1}{20}[/latex] and the x-axis where [latex]0 \lt x \lt 2[/latex].

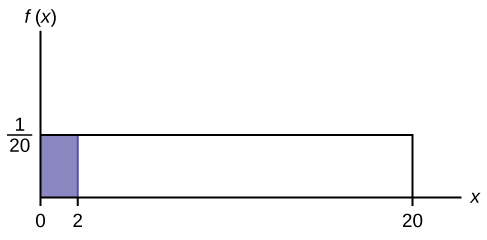
This shows the graph of the function f(x) = 1/20. A horizontal line ranges from the point (0, 1/20) to the point (20, 1/20). A vertical line extends from the x-axis to the end of the line at point (20, 1/20) creating a rectangle. A region is shaded inside the rectangle from x = 0 to x = 2.

[latex]\text{AREA}=(2–0)(\frac{1}{20})=0.1[/latex]

[latex](2–0)=2=\text{base of a rectangle}[/latex]

Reminder: area of a rectangle = (base)(height).

The area corresponds to a probability. The probability that [latex]x[/latex] is between zero and two is 0.1, which can be written mathematically as [latex]P(0 \lt x \lt 2) = P(x \lt 2) = 0.1[/latex].

Suppose we want to find the area between [latex]f(x) = \frac{1}{20}[/latex] and the x-axis where [latex]4 \lt x \lt 15[/latex].

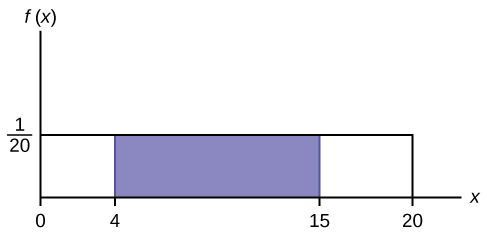
This shows the graph of the function f(x) = 1/20. A horizontal line ranges from the point (0, 1/20) to the point (20, 1/20). A vertical line extends from the x-axis to the end of the line at point (20, 1/20) creating a rectangle. A region is shaded inside the rectangle from x = 4 to x = 15.

[latex]\text{AREA} = (15 - 4)(\frac{1}{20}) = 0.55[/latex]

The area corresponds to the probability [latex]P(4 \lt x \lt 15) = 0.55[/latex].

Suppose we want to find [latex]P(x = 15)[/latex]. On an x-y graph, [latex]x = 15[/latex] is a vertical line. A vertical line has no width (or zero width). Therefore, [latex]P(x = 15) = (\text{base})(\text{height}) = (0)(\frac{1}{20}) = 0[/latex].

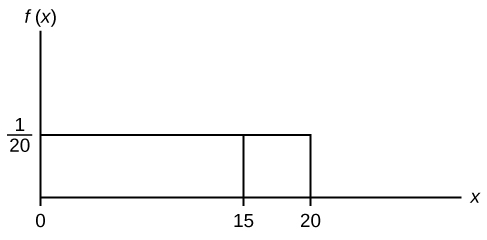
This shows the graph of the function f(x) = 1/20. A horizontal line ranges from the point (0, 1/20) to the point (20, 1/20). A vertical line extends from the x-axis to the end of the line at point (20, 1/20) creating a rectangle. A vertical line extends from the horizontal axis to the graph at x = 15.

[latex]P(X \le x)[/latex] (can be written as [latex]P(X \lt x)[/latex] for continuous distributions) is called the cumulative distribution function or CDF. Notice the “less than or equal to” symbol. We can use the CDF to calculate [latex]P(X > x)[/latex]. The CDF gives “area to the left” and [latex]P(X > x)[/latex] gives “area to the right.” We calculate [latex]P(X > x)[/latex] for continuous distributions as follows: [latex]P(X > x) = 1 – P (X \lt x)[/latex].

This shows the graph of the function f(x) = 1/20. A horizontal line ranges from the point (0, 1/20) to the point (20, 1/20). A vertical line extends from the x-axis to the end of the line at point (20, 1/20) creating a rectangle. The area to the left of a value, x, is shaded.

Label the graph with [latex]f(x)[/latex] and [latex]x[/latex]. Scale the x and y axes with the maximum x and y values. [latex]f(x) = \frac{1}{20}[/latex], [latex]0 \lt x \lt 20[/latex].

To calculate the probability that x is between two values, look at the following graph. Shade the region between [latex]x = 2.3[/latex] and [latex]x = 12.7[/latex]. Then calculate the shaded area of a rectangle.

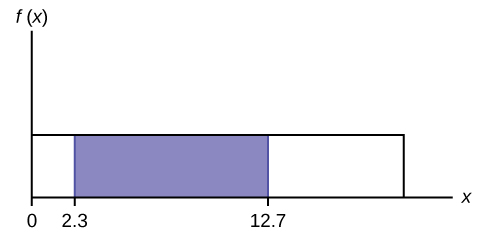
This shows the graph of the function f(x) = 1/20. A horizontal line ranges from the point (0, 1/20) to the point (20, 1/20). A vertical line extends from the x-axis to the end of the line at point (20, 1/20) creating a rectangle. A region is shaded inside the rectangle from x = 2.3 to x = 12.7

[latex]P(2.3 \lt x \lt 12.7 ) = ( \text{base} ) ( \text{height} ) = ( 12.7-2.3 ) ( \frac{1}{20} ) = 0.52[/latex]

Your Turn!

Consider the function [latex]f(x) = \frac{1}{8}[/latex] for [latex]0 \le x \le 8[/latex]. Draw the graph of [latex]f(x)[/latex] and find [latex]P(2.5 \lt x \lt 7.5)[/latex].

Solution

[latex]P (2.5 \lt x \lt 7.5) = 0.625[/latex]

 

Section 5.1 Review

The probability density function (pdf) is used to describe probabilities for continuous random variables. The area under the density curve between two points corresponds to the probability that the variable falls between those two values. In other words, the area under the density curve between points [latex]a[/latex] and [latex]b[/latex] is equal to [latex]P(a \lt x \lt b)[/latex]. The cumulative distribution function (cdf) gives the probability as an area. If [latex]X[/latex] is a continuous random variable, the probability density function (pdf), [latex]f(x)[/latex], is used to draw the graph of the probability distribution. The total area under the graph of f(x) is one. The area under the graph of [latex]f(x)[/latex] and between values a and b gives the probability [latex]P(a \lt x \lt b)[/latex].

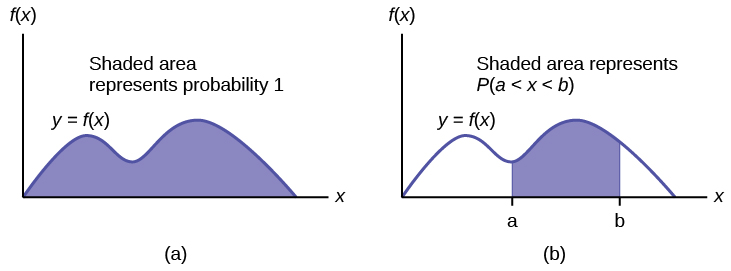
The graph on the left shows a general density curve, y = f(x). The region under the curve and above the x-axis is shaded. The area of the shaded region is equal to 1. This shows that all possible outcomes are represented by the curve. The graph on the right shows the same density curve. Vertical lines x = a and x = b extend from the axis to the curve, and the area between the lines is shaded. The area of the shaded region represents the probability that a value x falls between a and b.

The cumulative distribution function (cdf) of [latex]X[/latex] is defined by [latex]P (X \le x)[/latex]. It is a function of [latex]x[/latex] that gives the probability that the random variable is less than or equal to [latex]x[/latex].

Formula Review

Probability density function (pdf) [latex]f(x)[/latex]:

  • [latex]f(x) \ge 0[/latex]
  • The total area under the curve [latex]f(x)[/latex] is one.

Cumulative distribution function (cdf): [latex]P(X \le x)[/latex]

Section 5.1 Practice

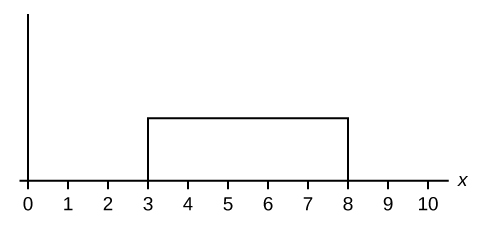
Which type of distribution does the graph illustrate?

The horizontal axis ranges from 0 to 10. The distribution is modeled by a rectangle extending from x = 3 to x =8.
Solution

Uniform Distribution

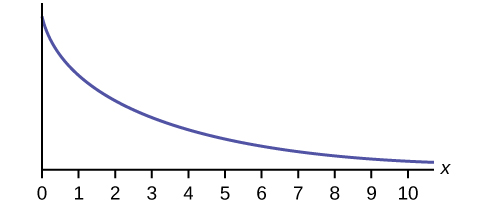
Which type of distribution does the graph illustrate?

This graph slopes downward. It begins at a point on the y-axis and approaches the x-axis at the right edge of the graph.

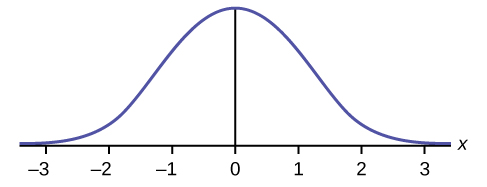
Which type of distribution does the graph illustrate?

This graph shows a bell-shaped graph. The symmetric graph reaches maximum height at x = 0 and slopes downward gradually to the x-axis on each side of the peak.
Solution

Normal Distribution

What does the shaded area represent? [latex]P(\underline{\hspace{2cm}} \lt x \lt \underline{\hspace{2cm}})[/latex]

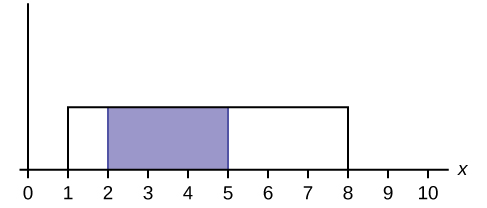
This graph shows a uniform distribution. The horizontal axis ranges from 0 to 10. The distribution is modeled by a rectangle extending from x = 1 to x = 8. A region from x = 2 to x = 5 is shaded inside the rectangle.

What does the shaded area represent? [latex]P(\underline{\hspace{2cm}} \lt x \lt \underline{\hspace{2cm}})[/latex]

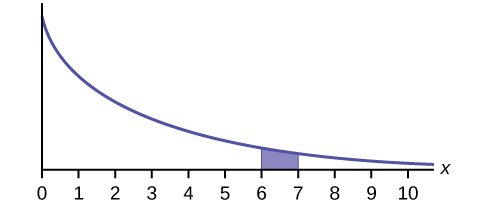
This graph shows an exponential distribution. The graph slopes downward. It begins at a point on the y-axis and approaches the x-axis at the right edge of the graph. The region under the graph from x = 6 to x = 7 is shaded.
Solution

[latex]P(6 \lt x \lt 7)[/latex]

For a continuous probability distribution, [latex]0 \le x \le 15[/latex]. What is [latex]P(x > 15)[/latex]?

What is the area under [latex]f(x)[/latex] if the function is a continuous probability density function?

Solution

one

For a continuous probability distribution, [latex]0 \le x \le 10[/latex]. What is [latex]P(x = 7)[/latex]?

A continuous probability function is restricted to the portion between [latex]x = 0 \text{ and } 7[/latex]. What is [latex]P(x = 10)[/latex]?

Solution

zero

[latex]f(x)[/latex] for a continuous probability function is [latex]\frac{1}{5}[/latex], and the function is restricted to [latex]0 \le x \le 5[/latex]. What is [latex]P(x \lt 0)[/latex]?

[latex]f(x)[/latex], a continuous probability function, is equal to [latex]\frac{1}{12}[/latex], and the function is restricted to [latex]0 \le x \le 12[/latex]. What is [latex]P (0 \lt x \lt 12)[/latex]?

Solution

one

Find the probability that [latex]x[/latex] falls in the shaded area.

Find the probability that [latex]x[/latex] falls in the shaded area.

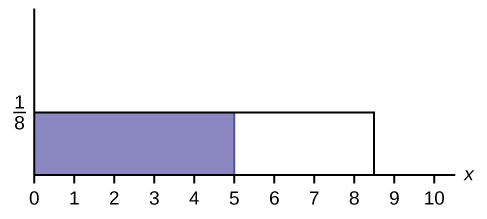
Solution

0.625

Find the probability that [latex]x[/latex] falls in the shaded area.

[latex]f(x)[/latex], a continuous probability function, is equal to [latex]\frac{1}{3}[/latex] and the function is restricted to [latex]1\le x \le 4[/latex]. Describe [latex]P (x>\frac{3}{2})[/latex].

Solution

The probability is equal to the area from [latex]x= \frac{3}{2}[/latex] to [latex]x = 4[/latex] above the x-axis and up to [latex]f(x) =\frac{1}{3}[/latex].

Consider the following experiment. You are one of 100 people enlisted to take part in a study to determine the percent of nurses in America with an R.N. (registered nurse) degree.  You ask nurses if they have an R.N. degree.  The nurses answer “yes” or “no.”  You then calculate the percentage of nurses with an R.N. degree.  You give that percentage to your supervisor.

  1. What part of the experiment will yield discrete data?
  2. What part of the experiment will yield continuous data?

When age is rounded to the nearest year, do the data stay continuous, or do they become discrete?  Why?

Solution

Age is a measurement, regardless of the accuracy used.

definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Introductory Statistics Copyright © 2024 by LOUIS: The Louisiana Library Network is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book