Chapter 9: Hypothesis Testing with Two Samples
Chapter 9 Homework
9.1 Homework
DIRECTIONS: For each of the word problems, use a solution sheet to do the hypothesis test. The solution sheet is found in Appendix E. Please feel free to make copies of the solution sheets. For the online version of the book, it is suggested that you copy the .doc or the .pdf files.
Note: If you are using a Student’s t-distribution for a homework problem in what follows, including for paired data, you may assume that the underlying population is normally distributed. (When using these tests in a real situation, you must first prove that assumption, however.)
The mean number of English courses taken in a two–year time period by male and female college students is believed to be about the same. An experiment is conducted and data are collected from 29 males and 16 females. The males took an average of three English courses with a standard deviation of 0.8. The females took an average of four English courses with a standard deviation of 1.0. Are the means statistically the same?
A student at a four-year college claims that mean enrollment at four–year colleges is higher than at two–year colleges in the United States. Two surveys are conducted. Of the 35 two–year colleges surveyed, the mean enrollment was 5,068 with a standard deviation of 4,777. Of the 35 four-year colleges surveyed, the mean enrollment was 5,466 with a standard deviation of 8,191.
Solution
Subscripts: 1: two-year colleges; 2: four-year colleges
a. [latex]H_0: \mu_1 \ge \mu_2[/latex]
b. [latex]H_a: \mu_1 \lt \mu_2[/latex]
c. [latex]{\overline{X}}_{1}–{\overline{X}}_{2}[/latex] is the difference between the mean enrollments of the two-year colleges and the four-year colleges.
d. Student’s-t
e. test statistic: -0.2480
f. p-value: 0.4019
g. Check student’s solution.
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Do not reject
iii. Reason for Decision: [latex]\text{p-value} > \alpha[/latex]
iv. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean enrollment at four-year colleges is higher than at two-year colleges.
At Rachel’s 11th birthday party, eight girls were timed to see how long (in seconds) they could hold their breath in a relaxed position. After a two-minute rest, they timed themselves while jumping. The girls thought that the mean difference between their jumping and relaxed times would be zero. Test their hypothesis.
| Relaxed time (seconds) | Jumping time (seconds) |
|---|---|
| 26 | 21 |
| 47 | 40 |
| 30 | 28 |
| 22 | 21 |
| 23 | 25 |
| 45 | 43 |
| 37 | 35 |
| 29 | 32 |
Mean entry-level salaries for college graduates with mechanical engineering degrees and electrical engineering degrees are believed to be approximately the same. A recruiting office thinks that the mean mechanical engineering salary is actually lower than the mean electrical engineering salary. The recruiting office randomly surveys 50 entry level mechanical engineers and 60 entry level electrical engineers. Their mean salaries were $46,100 and $46,700, respectively. Their standard deviations were $3,450 and $4,210, respectively. Conduct a hypothesis test to determine if you agree that the mean entry-level mechanical engineering salary is lower than the mean entry-level electrical engineering salary.
Solution
Subscripts: 1: mechanical engineering; 2: electrical engineering
a. [latex]H_0: \mu_1 \ge \mu_2[/latex]
b. [latex]H_a: \mu_1 \lt \mu_2[/latex]
c. [latex]{\overline{X}}_{1}-{\overline{X}}_{2}[/latex] is the difference between the mean entry level salaries of mechanical engineers and electrical engineers.
d. [latex]t_{108}[/latex]
e. test statistic: [latex]t = –0.82[/latex]
f. p-value: 0.2061
g. Check student’s solution.
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Do not reject the null hypothesis.
iii. Reason for Decision: [latex]\text{p-value} > \alpha[/latex]
iv. Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the mean entry-level salaries of mechanical engineers is lower than that of electrical engineers.
Marketing companies have collected data implying that teenage girls use more ringtones on their cellular phones than teenage boys do. In one particular study of 40 randomly chosen teenage girls and boys (20 of each) with cellular phones, the mean number of ringtones for the girls was 3.2 with a standard deviation of 1.5. The mean for the boys was 1.7 with a standard deviation of 0.8. Conduct a hypothesis test to determine if the means are approximately the same or if the girls’ mean is higher than the boys’ mean.
Use the following information to answer the next two exercises. The Eastern and Western Major League Soccer conferences have a new Reserve Division that allows new players to develop their skills. Data for a randomly picked date showed the following annual goals.
| Western | Eastern |
|---|---|
| Los Angeles 9 | D.C. United 9 |
| FC Dallas 3 | Chicago 8 |
| Chivas USA 4 | Columbus 7 |
| Real Salt Lake 3 | New England 6 |
| Colorado 4 | MetroStars 5 |
| San Jose 4 | Kansas City 3 |
Conduct a hypothesis test to answer the next two exercises.
1. The exact distribution for the hypothesis test is:
a. the normal distribution
b. the Student’s t-distribution
c. the uniform distribution
d. the exponential distribution
2. If the level of significance is 0.05, the conclusion is:
a. There is sufficient evidence to conclude that the W Division teams score fewer goals, on average, than the E teams
b. There is insufficient evidence to conclude that the W Division teams score more goals, on average, than the E teams.
c. There is insufficient evidence to conclude that the W teams score fewer goals, on average, than the E teams score.
d. Unable to determine
Solution
c
Suppose a statistics instructor believes that there is no significant difference between the mean class scores of statistics day students on Exam 2 and statistics night students on Exam 2. She takes random samples from each of the populations. The mean and standard deviation for 35 statistics day students were 75.86 and 16.91. The mean and standard deviation for 37 statistics night students were 75.41 and 19.73. The “day” subscript refers to the statistics day students. The “night” subscript refers to the statistics night students. A concluding statement is:
a. There is sufficient evidence to conclude that statistics night students’ mean on Exam 2 is better than the statistics day students’ mean on Exam 2.
b. There is insufficient evidence to conclude that the statistics day students’ mean on Exam 2 is better than the statistics night students’ mean on Exam 2.
c. There is insufficient evidence to conclude that there is a significant difference between the means of the statistics day students and night students on Exam 2.
d. There is sufficient evidence to conclude that there is a significant difference between the means of the statistics day students and night students on Exam 2.
Researchers interviewed street prostitutes in Canada and the United States. The mean age of the 100 Canadian prostitutes upon entering prostitution was 18 with a standard deviation of six. The mean age of the 130 United States prostitutes upon entering prostitution was 20 with a standard deviation of eight. Is the mean age of entering prostitution in Canada lower than the mean age in the United States? Test at a 1% significance level.
Solution
Test: two independent sample means, population standard deviations unknown.
Random variable: [latex]{\overline{X}}_{1}-{\overline{X}}_{2}[/latex]
Distribution: [latex]H_0: \mu_2= \mu_2; H_a: \mu_1 \lt \mu_2[/latex]
The mean age of entering prostitution in Canada is lower than the mean age in the United States.
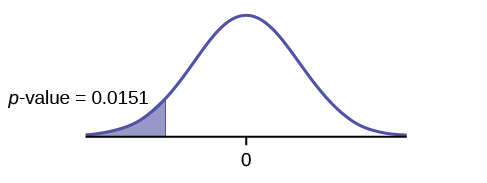
Graph: left-tailed
p-value : 0.0151
Decision: Do not reject [latex]H_0[/latex].
Conclusion: At the 1% level of significance, from the sample data, there is not sufficient evidence to conclude that the mean age of entering prostitution in Canada is lower than the mean age in the United States.
A powder diet is tested on 49 people, and a liquid diet is tested on 36 different people. Of interest is whether the liquid diet yields a higher mean weight loss than the powder diet. The powder diet group had a mean weight loss of 42 pounds with a standard deviation of 12 pounds. The liquid diet group had a mean weight loss of 45 pounds with a standard deviation of 14 pounds.
Suppose a statistics instructor believes that there is no significant difference between the mean class scores of statistics day students on Exam 2 and statistics night students on Exam 2. She takes random samples from each of the populations. The mean and standard deviation for 35 statistics day students were 75.86 and 16.91, respectively. The mean and standard deviation for 37 statistics night students were 75.41 and 19.73. The “day” subscript refers to the statistics day students. The “night” subscript refers to the statistics night students. An appropriate alternative hypothesis for the hypothesis test is:
a. [latex]\mu_{\text{day}} > \mu_{\text{night}}[/latex]
b. [latex]\mu_{\text{day}} /lt \mu_{\text{night}}[/latex]
c. [latex]\mu_{\text{day}} = \mu_{\text{night}}[/latex]
d. [latex]\mu_{\text{day}} \neq \mu_{\text{night}}[/latex]
Solution
d
9.2 Homework
DIRECTIONS: For each of the word problems, use a solution sheet to do the hypothesis test. The solution sheet is found in Appendix E. Please feel free to make copies of the solution sheets. For the online version of the book, it is suggested that you copy the .doc or the .pdf files.
A study is done to determine if students in the California state university system take longer to graduate, on average, than students enrolled in private universities. One hundred students from both the California state university system and private universities are surveyed. Suppose that from years of research, it is known that the population standard deviations are 1.5811 years and 1 year, respectively. The following data are collected. The California state university system students took on average 4.5 years with a standard deviation of 0.8. The private university students took on average 4.1 years with a standard deviation of 0.3.
Parents of teenage boys often complain that auto insurance costs more, on average, for teenage boys than for teenage girls. A group of concerned parents examines a random sample of insurance bills. The mean annual cost for 36 teenage boys was $679. For 23 teenage girls, it was $559. From past years, it is known that the population standard deviation for each group is $180. Determine whether or not you believe that the mean cost for auto insurance for teenage boys is greater than that for teenage girls.
Solution
Subscripts: 1 = boys, 2 = girls
a. [latex]H_0: \mu_1 \le \mu_2[/latex]
b. [latex]H_a: \mu_1 > \mu_2[/latex]
c. The random variable is the difference in the mean auto insurance costs for boys and girls.
d. normal
e. test statistic: [latex]z = 2.50[/latex]
f. p-value: 0.0062
g. Check student’s solution.
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Reject the null hypothesis.
iii. Reason for Decision: [latex]\text{p-value} \lt \alpha[/latex]
iv. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean cost of auto insurance for teenage boys is greater than that for girls.
A group of transfer bound students wondered if they will spend the same mean amount on texts and supplies each year at their four-year university as they have at their community college. They conducted a random survey of 54 students at their community college and 66 students at their local four-year university. The sample means were $947 and $1,011, respectively. The population standard deviations are known to be $254 and $87, respectively. Conduct a hypothesis test to determine if the means are statistically the same.
Some manufacturers claim that non-hybrid sedan cars have a lower mean miles-per-gallon (mpg) than hybrid ones. Suppose that consumers test 21 hybrid sedans and get a mean of 31 mpg with a standard deviation of seven mpg. Thirty-one non-hybrid sedans get a mean of 22 mpg with a standard deviation of four mpg. Suppose that the population standard deviations are known to be six and three, respectively. Conduct a hypothesis test to evaluate the manufacturers’ claim.
Solution
Subscripts: 1 = non-hybrid sedans, 2 = hybrid sedans
a. [latex]H_0: \mu_1 \ge \mu_2[/latex]
b. [latex]H_a: \mu_1 \lt \mu_2[/latex]
c. The random variable is the difference in the mean miles per gallon of non-hybrid sedans and hybrid sedans.
d. normal
e. test statistic: 6.36
f. p-value: 0
g. Check student’s solution.
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Reject the null hypothesis.
iii. Reason for decision: [latex]\text{p-value} \lt \alpha[/latex]
iv. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean miles per gallon of non-hybrid sedans is less than that of hybrid sedans.
A baseball fan wanted to know if there is a difference between the number of games played in a World Series when the American League won the series versus when the National League won the series. From 1922 to 2012, the population standard deviation of games won by the American League was 1.14, and the population standard deviation of games won by the National League was 1.11. Of 19 randomly selected World Series games won by the American League, the mean number of games won was 5.76. The mean number of 17 randomly selected games won by the National League was 5.42. Conduct a hypothesis test.
One of the questions in a study of marital satisfaction of dual-career couples was to rate the statement “I’m pleased with the way we divide the responsibilities for childcare.” The ratings went from one (strongly agree) to five (strongly disagree). The table below contains ten of the paired responses for husbands and wives. Conduct a hypothesis test to see if the mean difference in the husband’s versus the wife’s satisfaction level is negative (meaning that, within the partnership, the husband is happier than the wife).
| Wife’s Score | 2 | 2 | 3 | 3 | 4 | 2 | 1 | 1 | 2 | 4 |
| Husband’s Score | 2 | 2 | 1 | 3 | 2 | 1 | 1 | 1 | 2 | 4 |
Solution
a. [latex]H_0: \mu_d = 0[/latex]
b. [latex]H_a: \mu_d \lt 0[/latex]
c. The random variable [latex]X_d[/latex] is the average difference between husband’s and wife’s satisfaction level.
d. [latex]t_9[/latex]
e. test statistic: [latex]t = -1.86[/latex]
f. p-value: 0.0479
g. Check student’s solution
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Reject the null hypothesis, but run another test.
iii. Reason for Decision: [latex]\text{p-value} \lt \alpha[/latex]
iv. Conclusion: This is a weak test because alpha and the p-value are close. However, there is insufficient evidence to conclude that the mean difference is negative.
9.3 Homework
DIRECTIONS: For each of the word problems, use a solution sheet to do the hypothesis test. The solution sheet is found in [link]. Please feel free to make copies of the solution sheets. For the online version of the book, it is suggested that you copy the .doc or the .pdf files.
Note: If you are using a Student’s t-distribution for one of the following homework problems, including for paired data, you may assume that the underlying population is normally distributed. (In general, you must first prove that assumption, however.)
A recent drug survey showed an increase in the use of drugs and alcohol among local high school seniors as compared to the national percent. Suppose that a survey of 100 local seniors and 100 national seniors is conducted to see if the proportion of drug and alcohol use is higher locally than nationally. Locally, 65 seniors reported using drugs or alcohol within the past month, while 60 national seniors reported using them.
We are interested in whether the proportions of female suicide victims for ages 15 to 24 are the same for the whites and the blacks races in the United States. We randomly pick one year, 1992, to compare the races. The number of suicides estimated in the United States in 1992 for white females is 4,930. Five hundred eighty were aged 15 to 24. The estimate for black females is 330. Forty were aged 15 to 24. We will let female suicide victims be our population.
Solution
a. [latex]H_0: P_W = P_B[/latex]
b. [latex]H_a: P_W \neq P_B[/latex]
c. The random variable is the difference in the proportions of white and black suicide victims, aged 15 to 24.
d. normal for two proportions
e. test statistic: –0.1944
f. p-value: 0.8458
g. Check student’s solution.
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Reject the null hypothesis.
iii. Reason for decision: [latex]\text{p-value} \gt \alpha[/latex]
iv. Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the proportions of white and black female suicide victims, aged 15 to 24, are different.
Elizabeth Mjelde, an art history professor, was interested in whether the value from the Golden Ratio formula, [latex]\left(\frac{\text{larger + smaller dimension}}{\text{larger dimension}}\right)[/latex] was the same in the Whitney Exhibit for works from 1900 to 1919 as for works from 1920 to 1942. Thirty-seven early works were sampled, averaging 1.74 with a standard deviation of 0.11. Sixty-five of the later works were sampled, averaging 1.746 with a standard deviation of 0.1064. Do you think that there is a significant difference in the Golden Ratio calculation?
A recent year was randomly picked from 1985 to the present. In that year, there were 2,051 Hispanic students at Cabrillo College out of a total of 12,328 students. At Lake Tahoe College, there were 321 Hispanic students out of a total of 2,441 students. In general, do you think that the percent of Hispanic students at the two colleges is basically the same or different?
Solution
Subscripts: 1 = Cabrillo College, 2 = Lake Tahoe College
a. [latex]H_0: p_1 = p_2[/latex]
b. [latex]H_a: p_1 \neq p_2[/latex]
c. The random variable is the difference between the proportions of Hispanic students at Cabrillo College and Lake Tahoe College.
d. normal for two proportions
e. test statistic: 4.29
f. p-value: 0.00002
g. Check student’s solution.
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Reject the null hypothesis.
iii. Reason for decision: [latex]\text{p-value} \lt \alpha[/latex]
iv. Conclusion: There is sufficient evidence to conclude that the proportions of Hispanic students at Cabrillo College and Lake Tahoe College are different.
Use the following information to answer the next three exercises. Neuroinvasive West Nile virus is a severe disease that affects a person’s nervous system. It is spread by the Culex species of mosquito. In the United States in 2010 there were 629 reported cases of neuroinvasive West Nile virus out of a total of 1,021 reported cases and there were 486 neuroinvasive reported cases out of a total of 712 cases reported in 2011. Is the 2011 proportion of neuroinvasive West Nile virus cases more than the 2010 proportion of neuroinvasive West Nile virus cases? Using a 1% level of significance, conduct an appropriate hypothesis test.
a. a test of two proportions
b. a test of two independent means
c. a test of a single mean
d. a test of matched pairs.
2. An appropriate null hypothesis is:
a. [latex]p_{2011} \le p_{2010}[/latex]
b. [latex]p_{2011} \ge p_{2010}[/latex]
c. [latex]\mu_{2011} \le \mu_{2010}[/latex]
d. [latex]p_{2011} > p_{2010}[/latex]
Solution
a
3. The p-value is 0.0022. At a 1% level of significance, the appropriate conclusion is
a. There is sufficient evidence to conclude that the proportion of people in the United States in 2011 who contracted neuroinvasive West Nile disease is less than the proportion of people in the United States in 2010 who contracted neuroinvasive West Nile disease.
b. There is insufficient evidence to conclude that the proportion of people in the United States in 2011 who contracted neuroinvasive West Nile disease is more than the proportion of people in the United States in 2010 who contracted neuroinvasive West Nile disease.
c. There is insufficient evidence to conclude that the proportion of people in the United States in 2011 who contracted neuroinvasive West Nile disease is less than the proportion of people in the United States in 2010 who contracted neuroinvasive West Nile disease.
d. There is sufficient evidence to conclude that the proportion of people in the United States in 2011 who contracted neuroinvasive West Nile disease is more than the proportion of people in the United States in 2010 who contracted neuroinvasive West Nile disease.
Researchers conducted a study to find out if there is a difference in the use of eReaders by different age groups. Randomly selected participants were divided into two age groups. In the 16- to 29-year-old group, 7% of the 628 surveyed use eReaders, while 11% of the 2,309 participants 30 years old and older use eReaders.
Solution
Test: two independent sample proportions.
Random variable: p′1 – p′2
Distribution:
H0: p1 = p2
Ha: p1 ≠ p2
The proportion of eReader users is different for the 16- to 29-year-old users from that of the 30 and older users.
Graph: two-tailed
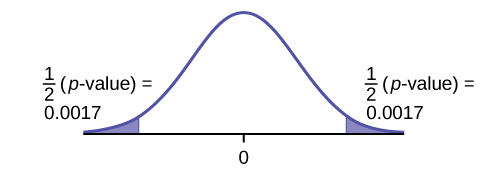
p-value : 0.0033
Decision: Reject the null hypothesis.
Conclusion: At the 5% level of significance, from the sample data, there is sufficient evidence to conclude that the proportion of eReader users 16 to 29 years old is different from the proportion of eReader users 30 and older.
Adults aged 18 years old and older were randomly selected for a survey on obesity. Adults are considered obese if their body mass index (BMI) is at least 30. The researchers wanted to determine if the proportion of women who are obese in the south is less than the proportion of southern men who are obese. The results are shown in [link]. Test at the 1% level of significance.
| Number who are obese | Sample size | |
|---|---|---|
| Men | 42,769 | 155,525 |
| Women | 67,169 | 248,775 |
Two computer users were discussing tablet computers. A higher proportion of people ages 16 to 29 use tablets than the proportion of people age 30 and older. The table below details the number of tablet owners for each age group. Test at the 1% level of significance.
| 16–29 year olds | 30 years old and older | |
|---|---|---|
| Own a Tablet | 69 | 231 |
| Sample Size | 628 | 2,309 |
Solution
Test: two independent sample proportions
Random variable: [latex]p^{\prime}_1 - p^{\prime}_2[/latex]
Distribution: [latex]H_0: p_1 = p_2; H_a: p_1 > p_2[/latex]
A higher proportion of tablet owners are aged 16 to 29 years old than are 30 years old and older.
Graph: right-tailed
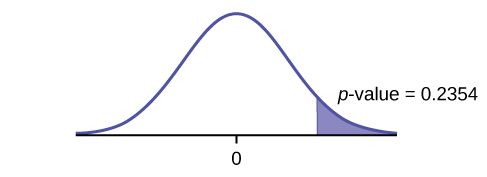
p-value: 0.2354
Decision: Do not reject [latex]H_0[/latex].
Conclusion: At the 1% level of significance, from the sample data, there is not sufficient evidence to conclude that a higher proportion of tablet owners are aged 16 to 29 years old than are 30 years old and older.
A group of friends debated whether more men use smartphones than women. They consulted a research study of smartphone use among adults. The results of the survey indicate that of the 973 men randomly sampled, 379 use smartphones. For women, 404 of the 1,304 who were randomly sampled use smartphones. Test at the 5% level of significance.
While her husband spent 2½ hours picking out new speakers, a statistician decided to determine whether the percentage of men who enjoy shopping for electronic equipment is higher than the percentage of women who enjoy shopping for electronic equipment. The population was Saturday afternoon shoppers. Out of 67 men, 24 said they enjoyed the activity. Eight of the 24 women surveyed claimed to enjoy the activity. Interpret the results of the survey.
Solution
Subscripts: 1: men; 2: women
a. [latex]H_0: p_1 \ge p_2[/latex]
b. [latex]H_a: p_1 > p_2[/latex]
c. [latex]{{P}^{\prime}}_{1}-{{P}^{\prime}}_{2}[/latex] is the difference between the proportions of men and women who enjoy shopping for electronic equipment.
d. normal for two proportions
e. test statistic: 0.22
f. p-value: 0.4133
g. Check student’s solution.
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Do not reject the null hypothesis.
iii. Reason for Decision: [latex]\text{p-value} > \alpha[/latex]
iv. Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the proportion of men who enjoy shopping for electronic equipment is more than the proportion of women.
We are interested in whether children’s educational computer software costs less, on average, than children’s entertainment software. Thirty-six educational software titles were randomly picked from a catalog. The mean cost was $31.14 with a standard deviation of $4.69. Thirty-five entertainment software titles were randomly picked from the same catalog. The mean cost was $33.86 with a standard deviation of $10.87. Decide whether children’s educational software costs less, on average, than children’s entertainment software.
Joan Nguyen recently claimed that the proportion of college-age males with at least one pierced ear is as high as the proportion of college-age females. She conducted a survey in her classes. Out of 107 males, 20 had at least one pierced ear. Out of 92 females, 47 had at least one pierced ear. Do you believe that the proportion of males has reached the proportion of females?
Solution
a. [latex]H_0: p_1 = p_2[/latex]
b. [latex]H_a: p_1 \neq p_2[/latex]
c. [latex]{{P}^{\prime }}_{1}-{{P}^{\prime }}_{2}[/latex] is the difference between the proportions of men and women that have at least one pierced ear.
d. normal for two proportions
e. test statistic: –4.82
f. p-value: 0
g. Check student’s solution.
h. i. [latex]\alpha: 0.05[/latex]
ii. Decision: Reject the null hypothesis.
iii. Reason for Decision: [latex]\text{p-value} \lt \alpha[/latex]
iv. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the proportions of males and females with at least one pierced ear is different.
9.4 Homework
DIRECTIONS: For each of the word problems, use a solution sheet to do the hypothesis test. The solution sheet is found in Appendix E. Please feel free to make copies of the solution sheets. For the online version of the book, it is suggested that you copy the .doc or the .pdf files.
Note: If you are using a Student’s t-distribution for the homework problems, including for paired data, you may assume that the underlying population is normally distributed. (When using these tests in a real situation, you must first prove that assumption, however.)
Ten individuals went on a low–fat diet for 12 weeks to lower their cholesterol. The data are recorded in the table below. Do you think that their cholesterol levels were significantly lowered?
| Starting cholesterol level | Ending cholesterol level |
|---|---|
| 140 | 140 |
| 220 | 230 |
| 110 | 120 |
| 240 | 220 |
| 200 | 190 |
| 180 | 150 |
| 190 | 200 |
| 360 | 300 |
| 280 | 300 |
| 260 | 240 |
Solution
p-value = 0.1494
At the 5% significance level, there is insufficient evidence to conclude that the medication lowered cholesterol levels after 12 weeks.
Use the following information to answer the next two exercises. A new AIDS prevention drug was tried on a group of 224 HIV positive patients. Forty-five patients developed AIDS after four years. In a control group of 224 HIV positive patients, 68 developed AIDS after four years. We want to test whether the method of treatment reduces the proportion of patients that develop AIDS after four years or if the proportions of the treated group and the untreated group stay the same.
Let the subscript t = treated patient and ut = untreated patient.
1. The appropriate hypotheses are:
a. [latex]H_0: p_t \lt p_{ut} and H_a: p_t \ge p_{ut}[/latex]
b. [latex]H_0: p_t \le p_{ut} and H_a: p_t > p_{ut}[/latex]
c. [latex]H_0: p_t = p_{ut} and H_a: p_t \neq p_{ut}[/latex]
d. [latex]H_0: p_t = p_{ut} and H_a: p_t \lt p_{ut}[/latex]
2. If the p-value is 0.0062 what is the conclusion (use [latex]\alpha = 0.05[/latex])?
a. The method has no effect.
b. There is sufficient evidence to conclude that the method reduces the proportion of HIV positive patients who develop AIDS after four years.
c. There is sufficient evidence to conclude that the method increases the proportion of HIV positive patients who develop AIDS after four years.
d. There is insufficient evidence to conclude that the method reduces the proportion of HIV positive patients who develop AIDS after four years.
Solution
b
Use the following information to answer the next two exercises. An experiment is conducted to show that blood pressure can be consciously reduced in people trained in a “biofeedback exercise program.” Six subjects were randomly selected and blood pressure measurements were recorded before and after the training. The difference between blood pressures was calculated (after – before) producing the following results: [latex]{\overline{x}}_{d} = -10.2; s_d = 8.4.[/latex] Using the data, test the hypothesis that the blood pressure has decreased after the training.
The distribution for the test is:
a. [latex]t_5[/latex]
b. [latex]t_6[/latex]
c. [latex]N(−10.2, 8.4)[/latex]
d. [latex]N(−10.2, \frac{8.4}{\sqrt{6}})[/latex]
If [latex]\alpha = 0.05[/latex], the p-value and the conclusion are
a. 0.0014; There is sufficient evidence to conclude that the blood pressure decreased after the training.
b. 0.0014; There is sufficient evidence to conclude that the blood pressure increased after the training.
c. 0.0155; There is sufficient evidence to conclude that the blood pressure decreased after the training.
d. 0.0155; There is sufficient evidence to conclude that the blood pressure increased after the training.
Solution
c
A golf instructor is interested in determining if her new technique for improving players’ golf scores is effective. She takes four new students. She records their 18-hole scores before learning the technique and then after having taken her class. She conducts a hypothesis test. The data are as follows.
| Player 1 | Player 2 | Player 3 | Player 4 | |
|---|---|---|---|---|
| Mean score before class | 83 | 78 | 93 | 87 |
| Mean score after class | 80 | 80 | 86 | 86 |
The correct decision is:
a. Reject [latex]H_0[/latex].
b. Do not reject the [latex]H_0[/latex].
A local cancer support group believes that the estimate for new female breast cancer cases in the south is higher in 2013 than in 2012. The group compared the estimates of new female breast cancer cases by southern state in 2012 and in 2013. The results are in the table below.
| Southern States | 2012 | 2013 |
|---|---|---|
| Alabama | 3,450 | 3,720 |
| Arkansas | 2,150 | 2,280 |
| Florida | 15,540 | 15,710 |
| Georgia | 6,970 | 7,310 |
| Kentucky | 3,160 | 3,300 |
| Louisiana | 3,320 | 3,630 |
| Mississippi | 1,990 | 2,080 |
| North Carolina | 7,090 | 7,430 |
| Oklahoma | 2,630 | 2,690 |
| South Carolina | 3,570 | 3,580 |
| Tennessee | 4,680 | 5,070 |
| Texas | 15,050 | 14,980 |
| Virginia | 6,190 | 6,280 |
Solution
Test: two matched pairs or paired samples (t-test)
Random variable: [latex]{\overline{X}}_{d}[/latex]
Distribution: [latex]t_{12}[/latex]
[latex]H_0: \mu_d = 0; H_a: \mu_d > 0[/latex]
The mean of the differences of new female breast cancer cases in the south between 2013 and 2012 is greater than zero. The estimate for new female breast cancer cases in the south is higher in 2013 than in 2012.
Graph: right-tailed
p-value: 0.0004
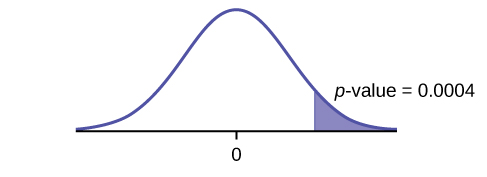
Decision: Reject [latex]H_0[/latex]
Conclusion: At the 5% level of significance, from the sample data, there is sufficient evidence to conclude that there was a higher estimate of new female breast cancer cases in 2013 than in 2012.
A traveler wanted to know if the prices of hotels are different in the ten cities that he visits the most often. The list of the cities with the corresponding hotel prices for his two favorite hotel chains is in the table below. Test at the 1% level of significance.
| Cities | Hyatt Regency prices in dollars | Hilton prices in dollars |
|---|---|---|
| Atlanta | 107 | 169 |
| Boston | 358 | 289 |
| Chicago | 209 | 299 |
| Dallas | 209 | 198 |
| Denver | 167 | 169 |
| Indianapolis | 179 | 214 |
| Los Angeles | 179 | 169 |
| New York City | 625 | 459 |
| Philadelphia | 179 | 159 |
| Washington, DC | 245 | 239 |
A politician asked his staff to determine whether the underemployment rate in the northeast decreased from 2011 to 2012. The results are in the table below.
| Northeastern States | 2011 | 2012 |
|---|---|---|
| Connecticut | 17.3 | 16.4 |
| Delaware | 17.4 | 13.7 |
| Maine | 19.3 | 16.1 |
| Maryland | 16.0 | 15.5 |
| Massachusetts | 17.6 | 18.2 |
| New Hampshire | 15.4 | 13.5 |
| New Jersey | 19.2 | 18.7 |
| New York | 18.5 | 18.7 |
| Ohio | 18.2 | 18.8 |
| Pennsylvania | 16.5 | 16.9 |
| Rhode Island | 20.7 | 22.4 |
| Vermont | 14.7 | 12.3 |
| West Virginia | 15.5 | 17.3 |
Solution
Test: matched or paired samples (t-test)
Difference data: {–0.9, –3.7, –3.2, –0.5, 0.6, –1.9, –0.5, 0.2, 0.6, 0.4, 1.7, –2.4, 1.8}
Random Variable: [latex]{\overline{X}}_{d}[/latex]
Distribution: [latex]H_0: \mu_d = 0; H_a: \mu_d \lt 0[/latex]
The mean of the differences of the rate of underemployment in the northeastern states between 2012 and 2011 is less than zero. The underemployment rate went down from 2011 to 2012.
Graph: left-tailed.
p-value: 0.1207
Decision: Do not reject [latex]H_0[/latex].
Conclusion: At the 5% level of significance, from the sample data, there is not sufficient evidence to conclude that there was a decrease in the underemployment rates of the northeastern states from 2011 to 2012.

